
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的点,
上的点,![]() 是线段
是线段![]() 上的点,且
上的点,且![]() .
.
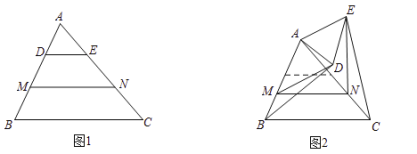
(1)观察猜想
如图1,若点![]() 是线段
是线段![]() 的三等分点,则
的三等分点,则![]() __________,
__________,![]() ___________.由此,我们猜想线段
___________.由此,我们猜想线段![]() ,
,![]() ,
,![]() ,
,![]() 之间满足的数量关系是_________.
之间满足的数量关系是_________.
(2)类比探究
将![]() 在平面内绕点
在平面内绕点![]() 按逆时针方向旋转一定的角度,连接
按逆时针方向旋转一定的角度,连接![]() ,
,![]() ,
,![]() ,
,![]() ,猜想在旋转的过程中,(1)中的结论是否仍然成立?若成立,请仅就图2的情形给出证明;若不成立,请说明理由.
,猜想在旋转的过程中,(1)中的结论是否仍然成立?若成立,请仅就图2的情形给出证明;若不成立,请说明理由.
(3)解决问题
将![]() 在平面内绕点
在平面内绕点![]() 自由旋转,若
自由旋转,若![]() ,请直接写出线段
,请直接写出线段![]() 的最大值.
的最大值.
 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】某校学生会为了解本校九年级学生体育测试中跳小绳成的情况,随机抽取了该校九年级若干名学生,调查他们的跳小绳成绩![]() (次1分),按成绩分成
(次1分),按成绩分成![]() ,
,![]() ,
,![]() ,
,![]() 五个等级.在本次调查中,男、女生的人数相同将所得数据绘制成如下的统计图:
五个等级.在本次调查中,男、女生的人数相同将所得数据绘制成如下的统计图:
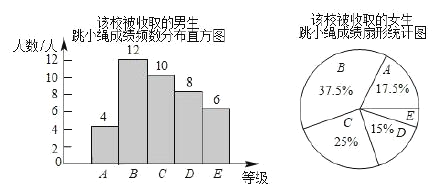
根据以上统计图提供的信息,解答下列问题:
(1)本次调查中,男生的跳小绳成绩的中位数在 等级;
(2)求本次调查中女生的跳小绳成绩为![]() 等级的人数:
等级的人数:
(3)若该校九年级共有男生400人,女生380人,估计该校九年级学生跳小绳成绩为![]() 等级的人数.
等级的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了实现伟大的强国复兴梦,全社会都在开展扫黑除恶专项斗争,某区为了解各学校老师对扫黑除恶应知应会知识的掌握情况,对甲、乙两个学校各180名老师进行了测试,从中各随机抽取30名教师的成绩(百分制),并对成绩(单位:分)进行整理、描述和分析,给出了部分成绩信息.

甲校参与测试的老师成绩在96≤x<98这一组的数据是:96,96.5,97,97.5,97,96.5,97.5,96,96.5,96.5,甲、乙两校参与测试的老师成绩的平均数、中位数、众数如下表:
学校 | 平均数 | 中位数 | 众数 |
甲校 | 96.35 | m | 99 |
乙校 | 95.85 | 97.5 | 99 |
根据以上信息,回答下列问题:
(1)m=________;
(2)在此次随机抽样测试中,甲校的王老师和乙校的李老师成绩均为97分,则他们在各自学校参与测试的老师中成绩的名次相比较更靠前的是________(选填王或李)老师,请写出理由;
(3)在此次随机测试中,乙校96分以上(含96分)的总人数比甲校96分以上(含96分)的总人数的2倍少100人,试估计乙校96分以上(含96分)的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,且
的直径,且![]() ,点
,点![]() 均在
均在![]() 上,
上,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
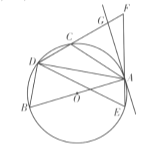
(1)求证:![]() .
.
(2)填空:
①当![]() __________,
__________,![]() 是等腰直角三角形;
是等腰直角三角形;
②当![]() __________,四边形
__________,四边形![]() 是平行四边形.
是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+mx﹣n的对称轴为x=2.若关于x的一元二次方程x2+mx﹣n=0在﹣1<x<6的范围内有实数解,则n的取值范围是( )
A.﹣4≤n<5B.n≥﹣4C.﹣4≤n<12D.5<n<12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,对角线AC、BD交于点O,E是BC延长线上一点,且AC=EC,连接AE交BD于点P.
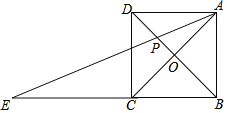
(1)求∠DAE的度数;
(2)求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个y与x的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.例如:y=![]() +1的图象向左平移2个单位,再向下平移1个单位得到y=
+1的图象向左平移2个单位,再向下平移1个单位得到y=![]() 的图象,则y=
的图象,则y=![]() +1是y与x的“反比例平移函数”.
+1是y与x的“反比例平移函数”.
(1)若(x+3)(y+2)=8,求y与x的函数表达式,并判断这个函数是否为“反比例平移函数”?
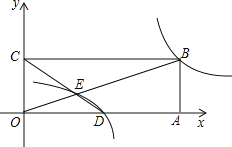
(2)如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A、C的坐标分别为(9,0)、(0,3),点D是OA的中点,连接OB、CD交于点E,“反比例平移函数”y=![]() 的图象经过B、E两点,则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
的图象经过B、E两点,则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
(3)在(2)的条件下,已知过线段BE中点的一条直线l交这个“反比例平移函数”图象于P、Q两点(P在Q的右侧),若B、E、P、Q为顶点组成的四边形面积为16,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中红球有2个,蓝球有1个,现从中任意摸出一个是红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸一个小球,请用画树状图或列表法求两次摸到都是红球的概率;
(3)若规定摸到红球得5分,摸到黄球得3分,摸到蓝球得1分,小明共摸6次小球(每次摸1个球,摸后放回)得20分,问小明有哪几种摸法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com