
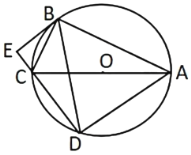
【题目】如图,![]() 为
为![]() 的直径,点
的直径,点![]() 、
、![]() 是
是![]() 上两点,
上两点,![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,![]() 的半径为5,求
的半径为5,求![]() 的值.
的值.
【答案】(1)证明见详解;(2)![]() .
.
【解析】
(1)连结OB和OD,证出OB∥DE,根据平行线的性质可以得到∠ECB=∠OBC,根据等腰三角形的性质可得∠OBC=∠BCA,从而得出![]() ;
;
(2)作CH⊥OB于H,解直角三角形求出BE,BC,再证明∠BDC=∠EBC,可得sin∠BDC=sin∠EBC=![]() ,即可解决问题.
,即可解决问题.

解:(1)连结OB和OD,
在△BOD和△BOA中,
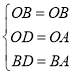
∴△BOD≌△BOA(SSS)
∴∠BDO=∠BAO
∵∠BDO=∠OBD,∠BAO=∠BDC
∴∠BDC=∠OBD
∴OB∥DE
∴∠ECB=∠OBC
∵∠OBC=∠BCA
∴∠ECB=∠BCA
(2)作CH⊥OB于H
由(1)知OB∥DE
∴∠HBE=∠E=90°
∵∠CHB=∠HBE=∠E=90°
∴四边形BECH是矩形
∴BH=CE=2
∵OA=OB=OC=5
∴OH=3,CH=BE=![]() =4
=4
∴BC=![]()
∵∠EBC+∠OBC=90°,∠OBC+∠OBA=90°
∴∠EBC=∠OBC
∵∠BDC=∠BAO=∠OBA
∴∠BDC=∠EBC
∴sin∠BDC=sin∠EBC=![]()
![]()
故答案为![]() .
.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
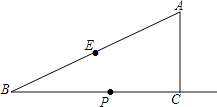
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+mx﹣n的对称轴为x=2.若关于x的一元二次方程x2+mx﹣n=0在﹣1<x<6的范围内有实数解,则n的取值范围是( )
A.﹣4≤n<5B.n≥﹣4C.﹣4≤n<12D.5<n<12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,对角线AC、BD交于点O,E是BC延长线上一点,且AC=EC,连接AE交BD于点P.
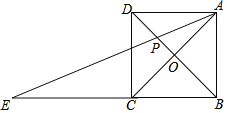
(1)求∠DAE的度数;
(2)求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
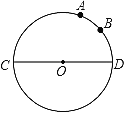
【题目】如图,CD是⊙O的直径,点A是半圆上的三等分点,B是弧AD的中点,P点为直线CD上的一个动点,当CD=6时,AP+BP的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个y与x的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.例如:y=![]() +1的图象向左平移2个单位,再向下平移1个单位得到y=
+1的图象向左平移2个单位,再向下平移1个单位得到y=![]() 的图象,则y=
的图象,则y=![]() +1是y与x的“反比例平移函数”.
+1是y与x的“反比例平移函数”.
(1)若(x+3)(y+2)=8,求y与x的函数表达式,并判断这个函数是否为“反比例平移函数”?
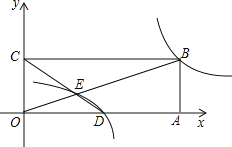
(2)如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A、C的坐标分别为(9,0)、(0,3),点D是OA的中点,连接OB、CD交于点E,“反比例平移函数”y=![]() 的图象经过B、E两点,则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
的图象经过B、E两点,则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
(3)在(2)的条件下,已知过线段BE中点的一条直线l交这个“反比例平移函数”图象于P、Q两点(P在Q的右侧),若B、E、P、Q为顶点组成的四边形面积为16,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
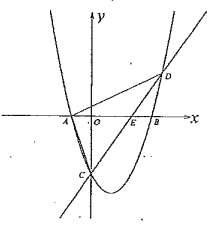
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() 连接
连接![]() 其中
其中![]() 点坐标
点坐标![]() .
.
(1)求抛物线的解析式;
(2)直线![]() 与抛物线交于点
与抛物线交于点![]() 与
与![]() 轴交于点
轴交于点![]() 求
求![]() 的面积;
的面积;
(3)在直线![]() 下方抛物线上有一点
下方抛物线上有一点![]() 过
过![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() .四边形
.四边形![]() 为平行四边形,求点
为平行四边形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于O点,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=![]() 上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).

(1)发现C船时,A、B、C三船所在位置的坐标分别为A(_______,_______)、B(_______,_______)和C(_______,_______);
(2)发现C船,三船立即停止训练,并分别从A、O、B三点出发沿最短路线同时前往救援,设A、B两船的速度相等,教练船与A船的速度之比为3:4,问教练船是否最先赶到?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com