
【题目】在数学实验课上,李静同学剪了两张直角三角形纸片,进行如下的操作:
操作一:如图1,将Rt△ABC纸片沿某条直线折叠,使斜边两个端点A与B重合,折痕为DE.
(1)如果AC=5cm,BC=7cm,可得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=1:2,可得∠B的度数为 ;
操作二:如图2,李静拿出另一张Rt△ABC纸片,将直角边AC沿直线CD折叠,使点A与点E重合,若AB=10cm,BC=8cm,请求出BE的长.

【答案】操作(一)(1)12cm.(2)36°;操作(二):2.8cm.
【解析】试题分析:操作一:(1)由翻折的性质可知:BD=AD,于是AD+DC=BC,从而可知△ACD的周长=BC+AC;
(2)设∠CAD=x,则∠BAD=2x,由翻折的性质可知∠CBA=2x,然后根据直角三角形两锐角互余可知:x+2x+2x=90°.
操作二:先利用勾股定理求得AC的长,然后利用面积法求得DC的长,在Rt△ACD中,利用勾股定理可求得AD的长,由翻折的性质可知:DE=DA,最后根据BE=AB﹣DE﹣AD计算即可.
解:操作一:(1)翻折的性质可知:BD=AD,
∴AD+DC=BC=7.
∴△ACD的周长=CD+AD+AC=BC+AC=7+5=12cm.
故答案为:12cm.
(2)设∠CAD=x,则∠BAD=2x.
由翻折的性质可知:∠BAD=∠CBA=2x,
∵∠B+∠BAC=90°,
∴x+2x+2x=90°.
解得;x=18°.
∴2x=2×18°=36°.
∴∠B=36°.
故答案为:36°.
操作二:在Rt△ABC中,AC=![]() =6.
=6.
由翻折的性质可知:ED=AD,DC⊥AB.
∵![]() ,
,
∴10CD=6×8.
∴CD=4.8.
在Rt△ADC中,AD=![]() =
=![]() =3.6.
=3.6.
∴EA=3.6×2=7.2.
∴BE=10﹣7.2=2.8.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】中国是世界上13个贫水国家之一.某校有800名在校学生,学校为鼓励学生节约用水,展开“珍惜水资源,节约每一滴水”系列教育活动,为响应学校号召,数学小组做了如下调查:
小亮为了解一个拧不紧的水龙头的滴水情况,记录了滴水时间和烧杯中的水面高度,如图1.小明设计了调查问卷,在学校随机抽取一部分学生进行了问卷调查,并制作出统计图.如图2和图3.结合图2和图3回答下列问题:

(1)参加问卷调查的学生人数为 60 人,其中选C的人数占调查人数的百分比为 .
(2)在这所学校中选“比较注意,偶尔水龙头滴水”的大概有 人.若在该校随机抽取一名学生,这名学生选B的概率为 .
请结合图1解答下列问题:
(3)在“水龙头滴水情况”图中,水龙头滴水量(毫升)与时间(分)可以用我们学过的哪种函数表示?请求出函数关系式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现,如图1,在正方形ABCD中,点E为CD的中点,过点D作AE的垂线,垂足为F与AC、BC分别交于点G,点H,则![]() = .
= .
(2)类比探究;如图2,在矩形ABCD中,![]() ,点E为CD的中点,过点D作AE的垂线,垂足为F,与AC、BC分别交于点G,点H,试探究
,点E为CD的中点,过点D作AE的垂线,垂足为F,与AC、BC分别交于点G,点H,试探究![]() 的值,并写出推理过程.
的值,并写出推理过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中, ![]() 厘米,
厘米, ![]() 厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______ 厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______ 厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A,B是数轴上的一点,AB=12,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数,经t秒后点P走过的路程为(用含t的代数式表示);
(2)若在动点P运动的同时另一动点Q从点B也出发,并以每秒4个单位长度的速度沿数轴向左匀速运动,问经多少时间点P就能追上点Q?
(3)若M为AP的中点,N为BP的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.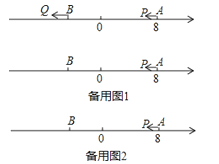
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列关于x的单项式,探究其规律:x,3x2 , 5x3 , 7x4 , 9x5 , 11x6 , ….按照上述规律,第2016个单项式是( )
A.4031x2015
B.4030x2016
C.4029x2015
D.4031x2016
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车从A地出发向南行驶了48千米后到达B地,又从B地向北行驶20千米到达C地,则A地与C地的距离是( ).
A.68千米
B.28千米
C.48千米
D.20千米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com