
【题目】在△ABC中,AB=AC,BC=8,D为边AC的中点.
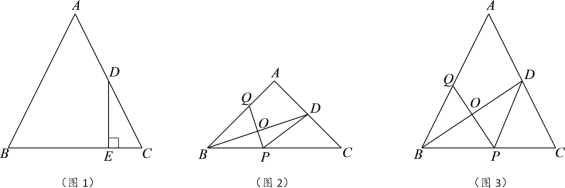
(1)如图1,过点D作DE⊥BC,垂足为点E,求线段CE的长;
(2)连接BD,作线段BD的垂直平分线分别交边BC、BD、AB于点P、O、Q.
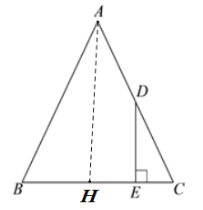
①如图2,当∠BAC=90°时,求BP的长;
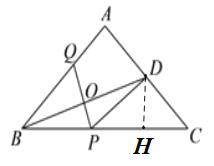
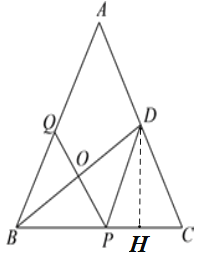
②如图3,设tan∠ABC=x,BP=y,求y与x之间的函数表达式和tan∠ABC的最大值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;② ![]() ;tan∠ABC有最大值为
;tan∠ABC有最大值为![]()
【解析】
(1)过点A作AH⊥BC交BC于点H,利用等腰三角形三线合一和平行线分线段成比例定理即可解决问题;
(2)①过点D作DH⊥BC交BC于点H,设![]() ,在
,在![]() 中利用勾股定理即可求解;
中利用勾股定理即可求解;
②过点D作DH⊥BC交BC于点H,同样在在![]() 中利用勾股定理即可表示出y与x之间的函数表达式,再根据当y有最大值时,x也有最大值,即tan∠ABC有最大值即可求解.
中利用勾股定理即可表示出y与x之间的函数表达式,再根据当y有最大值时,x也有最大值,即tan∠ABC有最大值即可求解.
(1)如图,过点A作AH⊥BC交BC于点H
∵![]() , BC=8
, BC=8
∴![]()
∵![]()
∴![]()
∵D为边AC的中点,
∴E为边CH的中点
∴![]()
(2)①过点D作DH⊥BC交BC于点H
∵PQ垂直平分BD
∴BP=PD
∵∠BAC=90°,AB=AC
∴![]()
∴![]()
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]()
解得![]() ,即
,即![]()
②过点D作DH⊥BC交BC于点H
∵PQ垂直平分BD
∴BP=PD
∵![]() ,tan∠ABC=tan∠ACB= x,BP=y
,tan∠ABC=tan∠ACB= x,BP=y
∴![]()
在![]() 中,
中,![]()
∴![]()
由![]() 得,
得,![]()
∴当y有最大值时,x也有最大值,即tan∠ABC有最大值.
∴当![]() 时,
时,![]()
解得![]() 或
或![]() (舍去)
(舍去)
∴tan∠ABC有最大值为![]()


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】抛物线![]() 中,函数值y与自变量
中,函数值y与自变量![]() 之间的部分对应关系如下表:
之间的部分对应关系如下表:
| … |
|
|
| 0 | 1 | … |
y | … |
|
| 0 |
|
| … |
(1)求该抛物线的表达式;
(2)如果将该抛物线平移,使它的顶点移到点M(2,4)的位置,那么其平移的方法是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一球,标号是1的概率;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
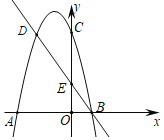
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C,D是二次函数图象上的一对对称点,一次函数的图象过点B,D,交y轴为E.
(1)求二次函数的解析式;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两把不同的锁和四把不同的钥匙,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁.现在任意取出一把钥匙去开任意一把锁.
(1)请用列表或画树状图的方法表示出上述试验所有可能结果;
(2)求一次打开锁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是

A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-4x-3,下列说法中正确的是( )
A.该函数图象的开口向下B.该函数图象的顶点坐标是(-2,-7)
C.当x<0时,y随x的增大而增大D.该函数图象与x轴有两个不同的交点,且分布在坐标原点两侧
查看答案和解析>>
科目:初中数学 来源: 题型:
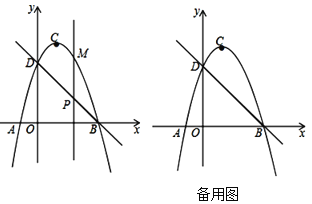
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 是抛物线的顶点.
是抛物线的顶点.
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的一个动点,其横坐标为
上方抛物线上的一个动点,其横坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,当线段
,当线段![]() 的长度最大时,求
的长度最大时,求![]() 的值及
的值及![]() 的最大值.
的最大值.
(3)在抛物线上是否存在异于![]() 、
、![]() 的点
的点![]() ,使
,使![]() 中
中![]() 边上的高为
边上的高为![]() ,若存在求出点
,若存在求出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com