
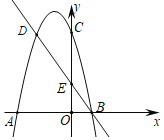
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C,D是二次函数图象上的一对对称点,一次函数的图象过点B,D,交y轴为E.
(1)求二次函数的解析式;
(2)求![]() 的值.
的值.
【答案】(1)y=﹣x2﹣2x+3;(2)![]() .
.
【解析】
(1)根据题意,设出抛物线的交点式,再根据抛物线过点C,可以求得该抛物线的解析式;
(2)根据(1)中的抛物线的解析式可以求得点D的坐标,从而可以求得直线BD的解析式,进而求得点E的坐标,再根据三角形相似,即可求得![]() 的值.
的值.
(1)设该函数的解析式为y=a(x+3)(x﹣1)
则3=a(0+3)(0﹣1),
解得,a=﹣1,
∴y=﹣(x+3)(x﹣1)=﹣x2﹣2x+3,
即二次函数的解析式;是y=﹣x2﹣2x+3;
(2)∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴该函数的对称轴是直线x=﹣1,
∵点C(0,3),点C,D是二次函数图象上的一对对称点,
∴点D的坐标为(﹣2,3),
设过点B(1,0)、点D(﹣2,3)的直线的函数解析式为y=kx+b,
![]() ,得
,得![]() ,
,
即直线BD的解析式为y=﹣x+1,
当x=0时,y=﹣0+1=0,
即点E的坐标为(0,1),
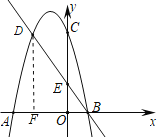
作DF⊥AB于点F,
∵DF⊥AB,EO⊥AB于点O,
∴△BEO∽△BDF,
∴![]() =
=![]() ,
,
∵点B(1,0),点F(﹣2,0),
∴BO=1,BF=3,
∴![]() =
=![]() ,
,
∴![]() =
=![]() .
.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
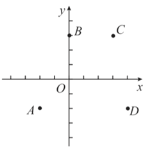
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,y是关于
,y是关于![]() 的二次函数,抛物线
的二次函数,抛物线![]() 经过点
经过点![]() .抛物线
.抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 则下列判断:
则下列判断:
①四条抛物线的开口方向均向下;
②当![]() 时,四条抛物线表达式中的
时,四条抛物线表达式中的![]() 均随
均随![]() 的增大而增大;
的增大而增大;
③抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 顶点的上方;
顶点的上方;
④抛物线![]() 与
与![]() 轴交点在点
轴交点在点![]() 的上方.
的上方.
其中正确的是
A.①②④B.①③④
C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
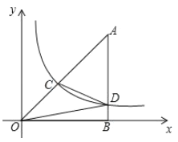
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 位于第一象限,点
位于第一象限,点![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴正半轴上,若双曲线
轴正半轴上,若双曲线![]()
![]() 与
与![]() 的边
的边![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 、
、![]() .若
.若![]() ,则
,则![]() 为_______________.
为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校旗杆的下方有一块圆形草坪,草坪的外面围着“圆环”水池,草坪和水池的外边缘是两个同心圆,旗杆在圆心O的位置且与地面垂直.
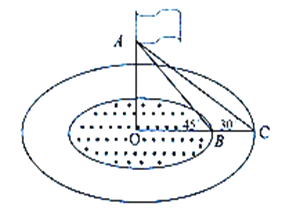
(1)若草坪的面积与圆环水池的面积之比为1∶4,求两个同心圆的半径之比.
(2)如图,若水池外面通往草坪有一座10米长的小桥BC,小桥所在的直线经过圆心O,上午8:00时太阳光线与地面成30°角,旗杆顶端的影子恰好落在水池的外缘;上午9:00时太阳光线与地面成45°角,旗杆顶端的影子恰好落在草坪的外缘,求旗杆的高OA长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,试探索线段BC,DC,EC之间满足的等量关系,并证明你的结论.
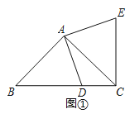
(2)如图②,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论.
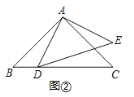
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,BC=8,D为边AC的中点.
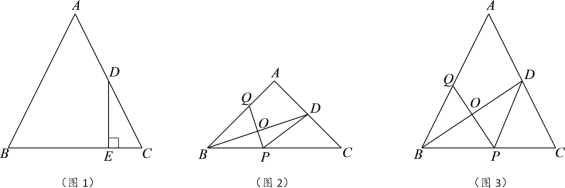
(1)如图1,过点D作DE⊥BC,垂足为点E,求线段CE的长;
(2)连接BD,作线段BD的垂直平分线分别交边BC、BD、AB于点P、O、Q.
①如图2,当∠BAC=90°时,求BP的长;
②如图3,设tan∠ABC=x,BP=y,求y与x之间的函数表达式和tan∠ABC的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
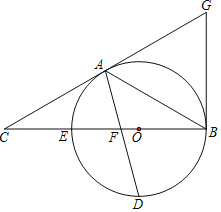
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC,
(1)求证:AC是⊙O的切线;
(2)若BF=8,DF=![]() ,求⊙O的半径.
,求⊙O的半径.
(3)过点B作⊙O的切线交CA的延长线于G,如果连接AE,将线段AC以直线AE为对称轴作对称线段AH,点H正好落在⊙O上,连接BH,求证:四边形AHBG为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)已知矩形AOCD在平面直角坐标系xOy中,∠CAO=60°,OA=2,B点的坐标为(2,0),动点M以每秒2个单位长度的速度沿A→C→B运动(M点不与点A、点B重合),设运动时间为t秒.
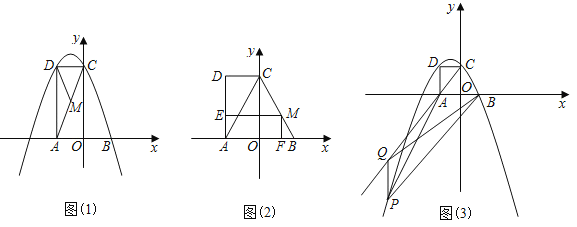
(1)求经过B、C、D三点的抛物线解析式;
(2)点P在(1)中的抛物线上,当M为AC中点时,若△PAM≌△PDM,求点P的坐标;
(3)当点M在CB上运动时,如图(2)过点M作ME⊥AD,MF⊥x轴,垂足分别为E、F,设矩形AEMF与△ABC重叠部分面积为S,求S与t的函数关系式,并求出S的最大值;
(4)如图(3)点P在(1)中的抛物线上,Q是CA延长线上的一点,且P、Q两点均在第三象限内,Q、A是位于直线BP同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2d,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com