
【题目】如图(1)已知矩形AOCD在平面直角坐标系xOy中,∠CAO=60°,OA=2,B点的坐标为(2,0),动点M以每秒2个单位长度的速度沿A→C→B运动(M点不与点A、点B重合),设运动时间为t秒.
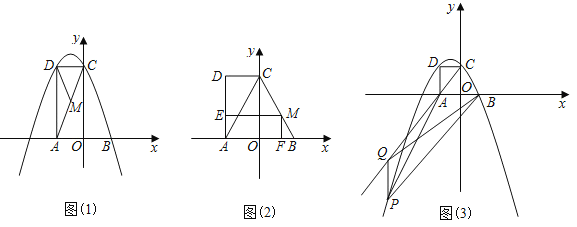
(1)求经过B、C、D三点的抛物线解析式;
(2)点P在(1)中的抛物线上,当M为AC中点时,若△PAM≌△PDM,求点P的坐标;
(3)当点M在CB上运动时,如图(2)过点M作ME⊥AD,MF⊥x轴,垂足分别为E、F,设矩形AEMF与△ABC重叠部分面积为S,求S与t的函数关系式,并求出S的最大值;
(4)如图(3)点P在(1)中的抛物线上,Q是CA延长线上的一点,且P、Q两点均在第三象限内,Q、A是位于直线BP同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2d,求点P的坐标.
【答案】(1)y= ![]() ;(2)点P(﹣1+
;(2)点P(﹣1+![]() ,
,![]() )或(﹣1﹣
)或(﹣1﹣![]() ,
,![]() );(3)S=﹣
);(3)S=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,当t=
,当t=![]() 时,S最大=
时,S最大=![]() ;(4)P(﹣8,-10
;(4)P(﹣8,-10![]() )
)
【解析】
(1)由直角三角形的性质可求点C,点D坐标,由待定系数法可求解析式;
(2)由全等三角形的性质可得DM=AM,PD=AP,可得点P在AD的垂直平分线上,可求点P的纵坐标,代入可求解;
(3)由题意可证△ACB是等边三角形,可得CM=2t-4,BF=![]() (8﹣2t)=4﹣t,MF=4
(8﹣2t)=4﹣t,MF=4![]() ﹣
﹣![]() t,AF=t,即可求重叠部分面积,由二次函数的性质可求解;
t,AF=t,即可求重叠部分面积,由二次函数的性质可求解;
(4)由题意先求出直线AC,BP的解析式,即可求点P坐标.
解:(1)∵四边形ABCD是矩形,
∴CD=AO=2,∠AOC=90°,且∠CAO=60°,OA=2,
∴OC=2![]() ,
,
∴点C(0,2![]() ),点D(﹣2,2
),点D(﹣2,2![]() ),
),
设抛物线解析式为y=a(x+1)2+c,代B(2,0),C(0,2![]() )
)
∴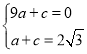
解得: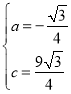
∴抛物线解析式为y=﹣![]() (x+1)2+
(x+1)2+![]() =
=![]() ,
,
(2)∵M为AC中点,
∴MA=MD,
∵△PAM≌△PDM,
∴PA=PD,
∴点P在AD的垂直平分线上
∴点P纵坐标为![]() ,
,
∴![]()
∴x1=﹣1+![]() ,x2=﹣1﹣
,x2=﹣1﹣![]()
∴点P(﹣1+![]() ,
,![]() )或(﹣1﹣
)或(﹣1﹣![]() ,
,![]() )
)
(3)如图2,
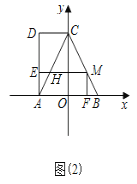
∵AO=BO=2,CO⊥AB,
∴AC=BC=4,∠CAO=60°,
∴△ACB是等边三角形,
由题意可得:CM=2t﹣4,BF=![]() (8﹣2t)=4﹣t,MF=4
(8﹣2t)=4﹣t,MF=4![]() ﹣
﹣![]() t,AF=t.
t,AF=t.
∵四边形AEMF是矩形,
∴AE=MF,EM=AF,EM∥AB,
∴∠CMH=∠CBA=60°,∠CHM=∠CAO=60°,
∴△CMH是等边三角形,
∴CM=MH=2t﹣4,
∵S=![]() (2t﹣4+t)(4
(2t﹣4+t)(4![]() ﹣t)=﹣
﹣t)=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]()
当t=![]() 时,S最大=
时,S最大=![]() ,
,
(4)∵S△ABP=![]() ×4×d=2d,
×4×d=2d,
又S△BPQ=2d
∴S△ABP=S△BPQ,
∴AQ∥BP
设直线AC解析式为y=kx+b,
把A(﹣2,0),C(0,2![]() )代入其中,得
)代入其中,得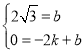
∴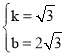
∴直线AC解析式为:y=![]() x+2
x+2![]() ,
,
设直线BP 的解析式为y=![]() x+n,把B(2,0)代入其中,得
x+n,把B(2,0)代入其中,得
0=2![]() +n,
+n,
∴b=﹣2![]()
∴直线BP解析式为:y=![]() x﹣2
x﹣2![]() ,
,
∴![]() =
=![]() x﹣2
x﹣2![]() ,
,
∴x1=2(舍去),x2=﹣8,
∴P(﹣8,-10![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
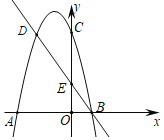
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C,D是二次函数图象上的一对对称点,一次函数的图象过点B,D,交y轴为E.
(1)求二次函数的解析式;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-4x-3,下列说法中正确的是( )
A.该函数图象的开口向下B.该函数图象的顶点坐标是(-2,-7)
C.当x<0时,y随x的增大而增大D.该函数图象与x轴有两个不同的交点,且分布在坐标原点两侧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某球室有三种品牌的![]() 个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知
个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知![]() (一次拿到
(一次拿到![]() 元球)
元球)![]() .
.
(1)求这![]() 个球价格的众数;
个球价格的众数;
(2)若甲组已拿走一个![]() 元球训练,乙组准备从剩余
元球训练,乙组准备从剩余![]() 个球中随机拿一个训练.
个球中随机拿一个训练.
①所剩的![]() 个球价格的中位数与原来
个球价格的中位数与原来![]() 个球价格的中位数是否相同?并简要说明理由;
个球价格的中位数是否相同?并简要说明理由;
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
又拿 先拿 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(m+1)x﹣m﹣2(m>0)与x轴交于A、B两点,与y轴交于点C,不论m取何正数,经过A、B、C三点的⊙P恒过y轴上的一个定点,则该定点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度 | …… | -4 | -2 | 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
由这些数据,科学家推测出植物每天高度增长量![]() 是温度
是温度![]() 的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度![]() 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 是抛物线的顶点.
是抛物线的顶点.
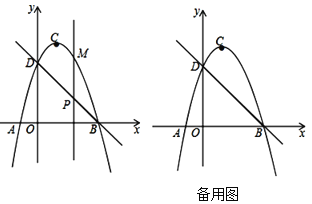
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的一个动点,其横坐标为
上方抛物线上的一个动点,其横坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,当线段
,当线段![]() 的长度最大时,求
的长度最大时,求![]() 的值及
的值及![]() 的最大值.
的最大值.
(3)在抛物线上是否存在异于![]() 、
、![]() 的点
的点![]() ,使
,使![]() 中
中![]() 边上的高为
边上的高为![]() ,若存在求出点
,若存在求出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
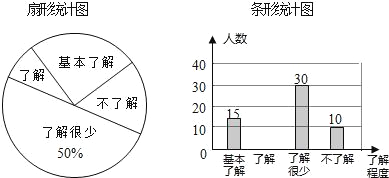
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com