
����Ŀ��ij����������Ʒ�Ƶ�![]() ��ƹ���۸���7��8��9����λ��Ԫ�����֣���������ó�һ������֪
��ƹ���۸���7��8��9����λ��Ԫ�����֣���������ó�һ������֪![]() ��һ���õ�
��һ���õ�![]() Ԫ��
Ԫ��![]() ��
��
��1������![]() ����۸��������
����۸��������
��2��������������һ��![]() Ԫ��ѵ������������ʣ��
Ԫ��ѵ������������ʣ��![]() �����������һ��ѵ����
�����������һ��ѵ����
����ʣ��![]() ����۸����λ����ԭ��
����۸����λ����ԭ��![]() ����۸����λ���Ƿ���ͬ������Ҫ˵�����ɣ�
����۸����λ���Ƿ���ͬ������Ҫ˵�����ɣ�
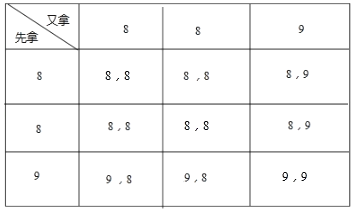
������������ó�һ�����Żأ�֮���������һ�������б�������ͼ�����������ζ��õ�8Ԫ��ĸ��ʣ�
���� ���� | |||
���𰸡���1����![]() ����۸������Ϊ
����۸������Ϊ![]() Ԫ����2������ʣ��
Ԫ����2������ʣ��![]() ����۸����λ����ԭ��
����۸����λ����ԭ��![]() ����۸����λ����ͬ�����������ζ��õ�
����۸����λ����ͬ�����������ζ��õ�![]() Ԫ��ĸ���Ϊ
Ԫ��ĸ���Ϊ![]() ��
��
��������
��1���ɸ��ʹ�ʽ���8Ԫ��ĸ������������Ķ��弴�ɵó��𰸣�
��2��������λ���Ķ��弴�ɵó��𰸣�
�����б����ó����н�����������ζ��õ�8Ԫ��Ľ����4�����ɸ��ʹ�ʽ���ɵó��𰸣�
��1����P��һ���õ�8Ԫ��![]() ����8Ԫ��ĸ���Ϊ4
����8Ԫ��ĸ���Ϊ4![]() 2�����������մ�С�����˳������Ϊ7��8��8��9������4����۸������Ϊ8Ԫ��
2�����������մ�С�����˳������Ϊ7��8��8��9������4����۸������Ϊ8Ԫ��
��2������ʣ��3����۸����λ����ԭ��4����۸����λ����ͬ���������£�
ԭ��4����ļ۸��մ�С�����˳������Ϊ7��8��8��9����ԭ��4����۸����λ��Ϊ![]() 8��Ԫ������ʣ��3����۸�Ϊ8��8��9������ʣ��3����۸����λ��Ϊ8Ԫ������ʣ��3����۸����λ����ԭ��4����۸����λ����ͬ��
8��Ԫ������ʣ��3����۸�Ϊ8��8��9������ʣ��3����۸����λ��Ϊ8Ԫ������ʣ��3����۸����λ����ԭ��4����۸����λ����ͬ��
���б���ͼ��ʾ������9���ȿ��ܵĽ�����������ζ��õ�8Ԫ��Ľ����4�������������ζ��õ�8Ԫ��ĸ���Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ѧУ��˵��·���һ��Բ�β�ƺ����ƺ������Χ����Բ����ˮ�أ���ƺ��ˮ�ص����Ե������ͬ��Բ�������Բ��O��λ��������洹ֱ.
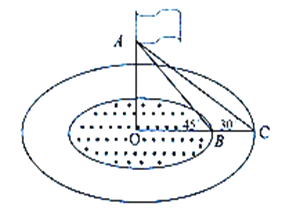
��1������ƺ�������Բ��ˮ�ص����֮��Ϊ1��4��������ͬ��Բ�İ뾶֮��.
��2����ͼ����ˮ������ͨ����ƺ��һ��10�׳���С��BC��С�����ڵ�ֱ�߾���Բ��O������8:00ʱ̫������������30���ǣ���˶��˵�Ӱ��ǡ������ˮ�ص���Ե������9:00ʱ̫������������45���ǣ���˶��˵�Ӱ��ǡ�����ڲ�ƺ����Ե������˵ĸ�OA��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
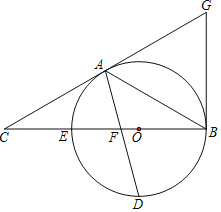
����Ŀ����ͼ������ABC��BC����һ��OΪԲ�ĵ�Բ������A��B���㣬����BC�߽��ڵ�E��DΪBE���°�Բ�����е㣬����AD��BC��F����AC��FC��
��1����֤��AC�ǡ�O�����ߣ�
��2����BF��8��DF��![]() �����O�İ뾶��
�����O�İ뾶��
��3������B����O�����߽�CA���ӳ�����G���������AE�����߶�AC��ֱ��AEΪ�Գ������Գ��߶�AH����H�������ڡ�O�ϣ�����BH����֤���ı���AHBGΪ���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C��D���߶�AB�ϣ��ҡ�PCD�ǵȱ������Σ���APB��120�㣮
��1����֤����ACP�ס�PDB��
��2����AC��4��BD��9ʱ������CD��ֵ��
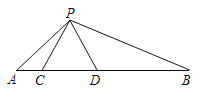
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��һ���̻�����������Ӱ����EOFB��GHMN���������εĻ��ԣ���֪���ɷ����С�������������̻����ϣ���С�����ڻ����ϵĸ���Ϊ��������
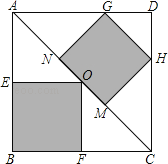
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����κ���y����x2+2x+3��ͼ��x���ڵ�A��B����A�ڵ�B����ࣩ�����ѵ�B����ƽ��m��m��0������λ���ȵõ�B1������B1����ƽ��n��n��0������λ���ȣ�����ö��κ���ͼ���ϵĵ�B2�غϣ�����B1����ƽ�ƣ�n+2������λ���ȣ�����ö��κ���ͼ���ϵĵ�B3�غϣ���n��ֵΪ��������
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����֪����AOCD��ƽ��ֱ������ϵxOy�У���CAO��60����OA��2��B�������Ϊ��2��0��������M��ÿ��2����λ���ȵ��ٶ���A��C��B�˶���M�㲻���A����B�غϣ������˶�ʱ��Ϊt�룮
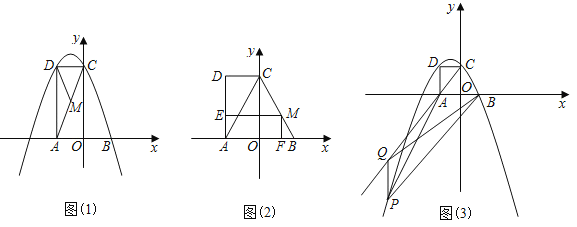
��1����B��C��D����������߽���ʽ��
��2����P�ڣ�1���е��������ϣ���MΪAC�е�ʱ������PAM�ա�PDM�����P�����ꣻ
��3������M��CB���˶�ʱ����ͼ��2������M��ME��AD��MF��x�ᣬ����ֱ�ΪE��F�������AEMF����ABC�ص��������ΪS����S��t�ĺ�����ϵʽ�������S�����ֵ��
��4����ͼ��3����P�ڣ�1���е��������ϣ�Q��CA�ӳ����ϵ�һ�㣬��P��Q������ڵ��������ڣ�Q��A��λ��ֱ��BPͬ��IJ�ͬ���㣬����P��x��ľ���Ϊd����QPB�����Ϊ2d�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ��������ƽ��ÿ������۳�20����ÿ��ӯ��40Ԫ��Ϊ��������ӯ����С��棬�̳�������ȡ�ʵ��Ľ��۴�ʩ����Ҫ��ÿ��ӯ��������20Ԫ�������鷢�֡���ÿ������ÿ����1Ԫ�����̳�ÿ��ɶ�����2��.
��1����ÿ����������4Ԫ����ÿ���ӯ������Ԫ��
��2�����̳�ƽ��ÿ��ӯ��1200Ԫ����ÿ������Ӧ���۶���Ԫ��
��3�����̳�Ϊ����Ч�������ÿ������Ӧ���۶���Ԫʱ���̳�ƽ��ÿ��ӯ����ࣿÿ�����ӯ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����κ���ͼ��Ķ��������ǣ�3��5�����������߾�����A��1��3����
��1����������ߵı���ʽ��
��2�������A���ڸ������߶Գ���ĶԳƵ���B�㣬����������y��Ľ�����C�㣬���ABC�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com