
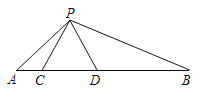
【题目】如图,点C、D在线段AB上,且△PCD是等边三角形.∠APB=120°.
(1)求证:△ACP∽△PDB;
(2)当AC=4,BD=9时,试求CD的值.
【答案】(1)详见解析;(2)6.
【解析】
(1)先证明∠ACP=∠PDB=120°,然后由∠A+∠B=60°,∠DPB+∠B=60°可证明∠A=∠DPB,从而可证明△ACP∽△PDB.
(2)由相似三角形的性质得到![]() ,根据等边三角形的性质得到PC=PD=CD,等量代换得到
,根据等边三角形的性质得到PC=PD=CD,等量代换得到![]() ,即可得到答案.
,即可得到答案.
(1)证明:∵△PCD为等边三角形,
∴∠PCD=∠PDC=60°.
∴∠ACP=∠PDB=120°.
∵∠APB=120°,
∴∠A+∠B=60°.
∵∠PDB=120°,
∴∠DPB+∠B=60°.
∴∠A=∠DPB.
∴△ACP∽△PDB.
(2)解:由(1)得△ACP∽△PDB,
∴![]() ,
,
∵△PCD是等边三角形,
∴PC=PD=CD,
∴![]() ,
,
∴CD2=ACBD.
∵AC=4,BD=9,
∴CD=6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,
,![]() 的顶点
的顶点![]() 与
与![]() 的斜边
的斜边![]() 的中点重合,将
的中点重合,将![]() 绕点
绕点![]() 旋转,旋转过程中,线段
旋转,旋转过程中,线段![]() 与线段
与线段![]() 相交于点
相交于点![]() ,射线
,射线![]() 与线段
与线段![]() 相交于点
相交于点![]() ,与射线
,与射线![]() 相交于点
相交于点![]() .
.
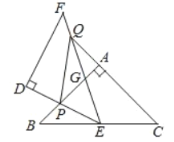
(1)求证:![]() ;
;
(2)求证:![]() 平分
平分![]() ;
;
(3)当![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两把不同的锁和四把不同的钥匙,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁.现在任意取出一把钥匙去开任意一把锁.
(1)请用列表或画树状图的方法表示出上述试验所有可能结果;
(2)求一次打开锁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-4x-3,下列说法中正确的是( )
A.该函数图象的开口向下B.该函数图象的顶点坐标是(-2,-7)
C.当x<0时,y随x的增大而增大D.该函数图象与x轴有两个不同的交点,且分布在坐标原点两侧
查看答案和解析>>
科目:初中数学 来源: 题型:
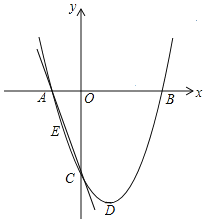
【题目】如图,抛物线y=ax2﹣2ax+c的图象经过点C(0,﹣2),顶点D的坐标为(1,﹣![]() ),与x轴交于A、B两点.
),与x轴交于A、B两点.
(1)求抛物线的解析式;
(2)连接AC,E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和![]() 的值.
的值.
(3)点F (0,y)是y轴上一动点,当y为何值时,![]() FC+BF的值最小.并求出这个最小值.
FC+BF的值最小.并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某球室有三种品牌的![]() 个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知
个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知![]() (一次拿到
(一次拿到![]() 元球)
元球)![]() .
.
(1)求这![]() 个球价格的众数;
个球价格的众数;
(2)若甲组已拿走一个![]() 元球训练,乙组准备从剩余
元球训练,乙组准备从剩余![]() 个球中随机拿一个训练.
个球中随机拿一个训练.
①所剩的![]() 个球价格的中位数与原来
个球价格的中位数与原来![]() 个球价格的中位数是否相同?并简要说明理由;
个球价格的中位数是否相同?并简要说明理由;
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
又拿 先拿 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度 | …… | -4 | -2 | 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
由这些数据,科学家推测出植物每天高度增长量![]() 是温度
是温度![]() 的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度![]() 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进货单价为30元的商品以每个40元的价格售出时,平均每月能售出600个,调查表明:这种商品的售价每上涨1元,其销售量就减少10个.
(1)为了使平均每月有10000元的销售利润且尽快售出,这种商品的售价应定为每个多少元?
(2)当该商品的售价为每个多少元时,商场销售该商品的平均月利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com