
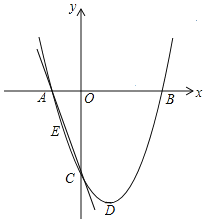
【题目】如图,抛物线y=ax2﹣2ax+c的图象经过点C(0,﹣2),顶点D的坐标为(1,﹣![]() ),与x轴交于A、B两点.
),与x轴交于A、B两点.
(1)求抛物线的解析式;
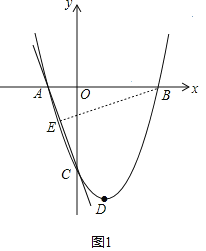
(2)连接AC,E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和![]() 的值.
的值.
(3)点F (0,y)是y轴上一动点,当y为何值时,![]() FC+BF的值最小.并求出这个最小值.
FC+BF的值最小.并求出这个最小值.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)点E(﹣
x﹣2;(2)点E(﹣![]() ,﹣
,﹣![]() ),
),![]() =
=![]() ;(3)﹣
;(3)﹣![]() ,
,![]() .
.
【解析】
(1)将点C、D的坐标代入抛物线表达式,即可求解;
(2)当△AOC∽△AEB时,![]() =(
=(![]() )2=(
)2=(![]() )2=
)2=![]() ,求出yE=﹣
,求出yE=﹣![]() ,由△AOC∽△AEB得:
,由△AOC∽△AEB得:![]() =
=![]() =
=![]() ,即可求解;
,即可求解;
(3)如图2,连接BF,过点F作FG⊥AC于G,当折线段BFG与BE重合时,取得最小值,即可求解.
解:(1)由题可列方程组: ,
,
解得:
∴抛物线解析式为:y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)∵抛物线y=![]() x2﹣
x2﹣![]() x﹣2的图象与x轴交于A、B两点,
x﹣2的图象与x轴交于A、B两点,
∴点A(﹣1,0),点B(3,0),
∴AO=1,BO=3,
∴∠AOC=90°,AC=![]() ,AB=4,
,AB=4,
设直线AC的解析式为:y=kx+b,
则![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为:y=﹣2x﹣2;
当△AOC∽△AEB时
∴![]() =(
=(![]() )2=(
)2=(![]() )2=
)2=![]() ,
,
∵S△AOC=1,
∴S△AEB=![]() ,
,
∴![]() AB×|yE|=
AB×|yE|=![]() ,AB=4,则yE=﹣
,AB=4,则yE=﹣![]() ,
,
则点E(﹣![]() ,﹣
,﹣![]() );
);
由△AOC∽△AEB得:![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ;
;
(3)如图2,连接BF,过点F作FG⊥AC于G,
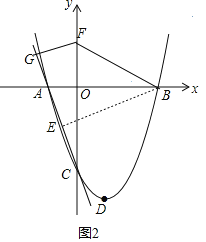
则FG=CFsin∠FCG=![]() CF,
CF,
∴![]() CF+BF=GF+BF≥BE,
CF+BF=GF+BF≥BE,
当折线段BFG与BE重合时,取得最小值,
由(2)可知∠ABE=∠ACO
∴BE=ABcos∠ABE=ABcos∠ACO=4×![]() =
=![]() ,
,
|y|=OBtan∠ABE=OBtan∠ACO=3×![]() =
=![]() ,
,
∴当y=﹣![]() 时,即点F(0,﹣
时,即点F(0,﹣![]() ),
),![]() CF+BF有最小值为
CF+BF有最小值为![]() .
.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】如图,为了测量山脚到塔顶的高度(即![]() 的长),某同学在山脚
的长),某同学在山脚![]() 处用测角仪测得塔顶
处用测角仪测得塔顶![]() 的仰角为
的仰角为![]() ,再沿坡度为
,再沿坡度为![]() 的小山坡前进400米到达点
的小山坡前进400米到达点![]() ,在
,在![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() .
.
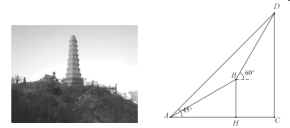
(1)求坡面![]() 的铅垂高度(即
的铅垂高度(即![]() 的长);
的长);
(2)求![]() 的长.(结果保留根号,测角仪的高度忽略不计).
的长.(结果保留根号,测角仪的高度忽略不计).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2.
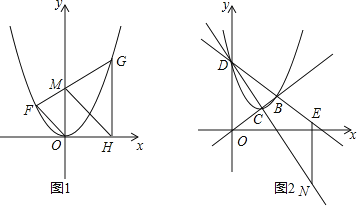
(1)在抛物线上有一点A(1,1),过点A的直线l与抛物线只有一个公共点,直接写出直线l的解析式;
(2)如图1,抛物线有两点F、G,连接FG交y轴于M,过G作x轴的垂线,垂足为H,连接HM、OF,求证:OF∥MH;
(3)将抛物线y=x2沿直线y=![]() x移动,新抛物线的顶点C,与直线的另一个交点为B,与y轴的交点为D,作直线x=4与直线CD、BD交于点N、E,如图2,求EN的长.
x移动,新抛物线的顶点C,与直线的另一个交点为B,与y轴的交点为D,作直线x=4与直线CD、BD交于点N、E,如图2,求EN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.求证:(1)∠A=∠GEF;(2)△BDF≌FEC.

查看答案和解析>>
科目:初中数学 来源: 题型:
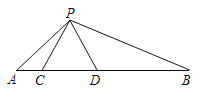
【题目】如图,点C、D在线段AB上,且△PCD是等边三角形.∠APB=120°.
(1)求证:△ACP∽△PDB;
(2)当AC=4,BD=9时,试求CD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有三张分别标有数字![]() 、
、![]() 、
、![]() 的卡片,它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为
的卡片,它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为![]() (不放回),再从中任意抽取一张,将上面的数字记为
(不放回),再从中任意抽取一张,将上面的数字记为![]() ,这样的数字
,这样的数字![]() ,
,![]() 能使关于
能使关于![]() 的一元二次方程
的一元二次方程![]() 有两个正根的概率为________.
有两个正根的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=﹣x2+2x+3的图象交x轴于点A、B(点A在点B的左侧).若把点B向上平移m(m>0)个单位长度得点B1,若点B1向左平移n(n>0)个单位长度,将与该二次函数图象上的点B2重合;若点B1向左平移(n+2)个单位长度,将与该二次函数图象上的点B3重合.则n的值为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某化工材料经销商购进一种化工材料若干千克,成本为每千克30元,物价部门规定其销售单价不低于成本价且不高于成本价的2倍,经试销发现,日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图所示.
(元)符合一次函数关系,如图所示.
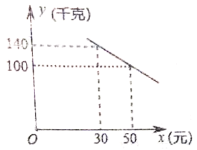
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若在销售过程中每天还要支付其他费用500元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
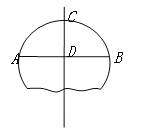
【题目】如图,破残的圆形轮片上,弦AB的垂直平分线交AB于C,交弦AB于D.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)若AB=24cm,CD=8cm,求(1)中所作圆的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com