
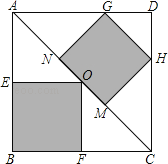
【题目】如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
设正方形ABCD的边长为a,根据正方形的性质∠ACB=∠ACD=45°,AC=![]() a,再利用四边形BEOF为正方形易得CF=OF=BF=
a,再利用四边形BEOF为正方形易得CF=OF=BF=![]() a,则S正方形BEOF=
a,则S正方形BEOF=![]() a2,设正方形MNGH的边长为x,易得CM=AN=MN=x,即3x=
a2,设正方形MNGH的边长为x,易得CM=AN=MN=x,即3x=![]() a,解得x=
a,解得x=![]() x,则S正方形MNGH=
x,则S正方形MNGH=![]() a2,然后根据几何概率的意义,用两个小正方形的面积和除以正方形ABCD的面积即可得到小鸟落在花圃上的概率,从而得到小鸟不落在花圃上的概率.
a2,然后根据几何概率的意义,用两个小正方形的面积和除以正方形ABCD的面积即可得到小鸟落在花圃上的概率,从而得到小鸟不落在花圃上的概率.
解:设正方形ABCD的边长为a,
∵四边形ABCD为正方形,
∴∠ACB=∠ACD=45°,AC=![]() a,
a,
∵四边形BEOF为正方形,
∴CF=OF=BF,
∴S正方形BEOF=(![]() a)2=
a)2=![]() a2,
a2,
设正方形MNGH的边长为x,
∵△ANG和△CMH都是等腰直角三角形,
∴CM=AN=MN=x,
∴3x=![]() a,解得x=
a,解得x=![]() a,
a,
∴S正方形MNGH=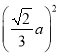 =
=![]() a2,
a2,
∴小鸟不落在花圃上的概率=1﹣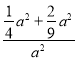 =
=![]()
故选:A.


科目:初中数学 来源: 题型:
【题目】甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一球,标号是1的概率;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是

A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-4x-3,下列说法中正确的是( )
A.该函数图象的开口向下B.该函数图象的顶点坐标是(-2,-7)
C.当x<0时,y随x的增大而增大D.该函数图象与x轴有两个不同的交点,且分布在坐标原点两侧
查看答案和解析>>
科目:初中数学 来源: 题型:
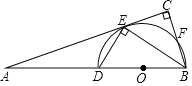
【题目】已知:如图,BD是半圆O的直径,A是BD延长线上的一点,BC⊥AE,交AE的延长线于点C,交半圆O于点F,且E为弧DF的中点.
(1)求证:AC是半圆O的切线;
(2)若BC=8,BE=6![]() ,求半径的长.
,求半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
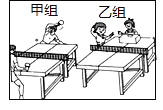
【题目】某球室有三种品牌的![]() 个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知
个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知![]() (一次拿到
(一次拿到![]() 元球)
元球)![]() .
.
(1)求这![]() 个球价格的众数;
个球价格的众数;
(2)若甲组已拿走一个![]() 元球训练,乙组准备从剩余
元球训练,乙组准备从剩余![]() 个球中随机拿一个训练.
个球中随机拿一个训练.
①所剩的![]() 个球价格的中位数与原来
个球价格的中位数与原来![]() 个球价格的中位数是否相同?并简要说明理由;
个球价格的中位数是否相同?并简要说明理由;
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
又拿 先拿 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(m+1)x﹣m﹣2(m>0)与x轴交于A、B两点,与y轴交于点C,不论m取何正数,经过A、B、C三点的⊙P恒过y轴上的一个定点,则该定点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 是抛物线的顶点.
是抛物线的顶点.
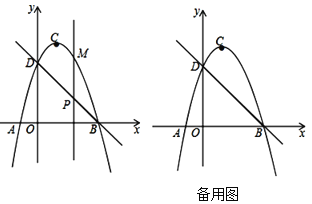
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的一个动点,其横坐标为
上方抛物线上的一个动点,其横坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,当线段
,当线段![]() 的长度最大时,求
的长度最大时,求![]() 的值及
的值及![]() 的最大值.
的最大值.
(3)在抛物线上是否存在异于![]() 、
、![]() 的点
的点![]() ,使
,使![]() 中
中![]() 边上的高为
边上的高为![]() ,若存在求出点
,若存在求出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为8,则GE+FH的最大值为( )
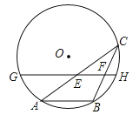
A.8B.12C.16D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com