
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,y是关于
,y是关于![]() 的二次函数,抛物线
的二次函数,抛物线![]() 经过点
经过点![]() .抛物线
.抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 则下列判断:
则下列判断:
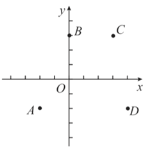
①四条抛物线的开口方向均向下;
②当![]() 时,四条抛物线表达式中的
时,四条抛物线表达式中的![]() 均随
均随![]() 的增大而增大;
的增大而增大;
③抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 顶点的上方;
顶点的上方;
④抛物线![]() 与
与![]() 轴交点在点
轴交点在点![]() 的上方.
的上方.
其中正确的是
A.①②④B.①③④
C.①②③D.②③④
 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】某服装店老板到厂家选购![]() 、
、![]() 两种品牌的羽绒服,
两种品牌的羽绒服,![]() 品牌羽绒服每件进价比
品牌羽绒服每件进价比![]() 品牌羽绒服每件进价多
品牌羽绒服每件进价多![]() 元,若用
元,若用![]() 元购进
元购进![]() 种羽绒服的数量是用
种羽绒服的数量是用![]() 元购进
元购进![]() 种羽绒服数量的
种羽绒服数量的![]() 倍.
倍.
(1)求![]() 、
、![]() 两种品牌羽绒服每件进价分别为多少元?
两种品牌羽绒服每件进价分别为多少元?
(2)若![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,
元,![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,服装店老板决定一次性购进
元,服装店老板决定一次性购进![]() 、
、![]() 两种品牌羽绒服共
两种品牌羽绒服共![]() 件,在这批羽绒服全部出售后所获利润不低于
件,在这批羽绒服全部出售后所获利润不低于![]() 元,则最少购进
元,则最少购进![]() 品牌羽绒服多少件?
品牌羽绒服多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
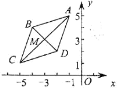
【题目】菱形ABCD在坐标平面内的位置如图所示,已知A(-1,5),D(-2,2),对角线交点M(-3,3),如果双曲线![]() (x<0)与菱形ABCD有公共点,那么k的取值范围是________
(x<0)与菱形ABCD有公共点,那么k的取值范围是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春天是放风筝的好时节,小明为了让风筝顺利起飞,特地将风筝放在坡度为1:2.4的山坡上,并站在视线刚好与风筝起飞点A齐平的B处,起风后小明开始往下跑26米至坡底C处,并继续沿平地向前跑16米到达D处后站在原地开始调整,小明将手中的线轴刚好举到与视线齐平处测得风筝的仰角是37°,此时风筝恰好升高到起飞时的正上方E处.已知小明视线距地面高度为1.5米,图中风筝E、A、B、C、D五点在同一平面,则风筝上升的垂直距离AE约为( )米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
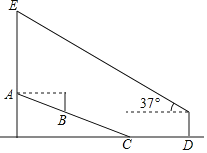
A.34.2B.32.7C.31.2D.22.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E为对角线AC上一点,连接DE,作EF⊥DE,交AD于点F,G为AD边上一点,且AB=AG,连接GE.
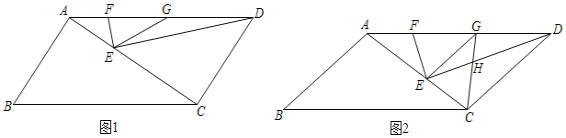
(1)如图1,若点G为DF的中点,AF=2,EG=4,∠B=60°,求AC的长;
(2)如图2,连接CG交DE于点H,若EG∥CD,∠ACB=∠DCG,求证:∠ECG=2∠AEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°.
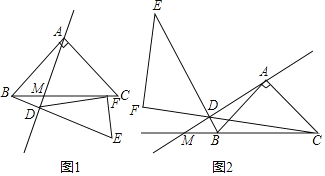
(1)如图1,若直线AD与BC相交于M,过点B作AM的垂线,垂足为D,连接CD并延长BD至E,使得DE=DC,过点E作EF⊥CD于F,证明:AD=EF+BD.
(2)如图2,若直线AD与CB的延长线相交于M,过点B作AM的垂线,垂足为D,连接CD并延长BD至E,使得DE=DC,过点E作EF⊥CD交CD的延长线于F,探究:AD、EF、BD之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
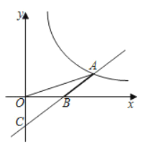
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为
为![]() 轴上一点,
轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某一广告墙PQ旁有两根直立的木杆AB和CD,某一时刻在太阳光下,木杆CD的影子刚好不落在广告墙PQ上.
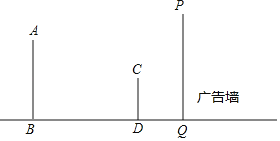
(1)画出太阳光线CE和AB的影子BF;
(2)若AB=10米,CD=6米,CD到PQ的距离DQ的长为8米,求此时木杆AB的影子BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
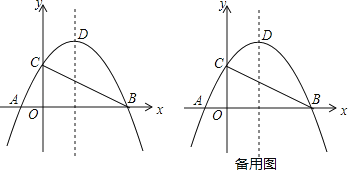
【题目】如图,抛物线y=﹣![]() x2+bx+c的图象经过点C,交x轴于点A(﹣1,0)、B(4,0)(A点在B点左侧),顶点为D.
x2+bx+c的图象经过点C,交x轴于点A(﹣1,0)、B(4,0)(A点在B点左侧),顶点为D.
(1)求抛物线的解析式;
(2)将△ABC沿直线BC对折,点A的对称点为A′,试求A′的坐标;
(3)抛物线的对称轴上是否存在点P,使∠BPC=∠BAC?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com