
【题目】如图,在□ABCD中,E为对角线AC上一点,连接DE,作EF⊥DE,交AD于点F,G为AD边上一点,且AB=AG,连接GE.
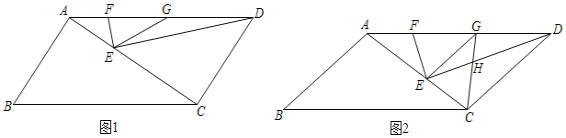
(1)如图1,若点G为DF的中点,AF=2,EG=4,∠B=60°,求AC的长;
(2)如图2,连接CG交DE于点H,若EG∥CD,∠ACB=∠DCG,求证:∠ECG=2∠AEF.
【答案】(1)AC=![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)过点C作CH⊥AD,交AD于点H,根据直角三角形斜边上的中线的性质得到FD和EG的长,即可得到AD的长,然后通过含有30°角的直角三角形的性质和勾股定理即可求出AC的长;
(2)根据平行四边形和∠ACB=∠DCG得到∠DAC=∠DCG,再根据全等三角形的判定和性质,三角形的外角性质,等边对等角及平行线的性质证明两角的倍数关系.
(1)如图,过点C作CH⊥AD,交AD于点H,
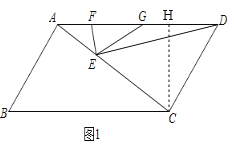
∵EF⊥DE,
∴△FED是直角三角形,
又G是斜边FD的中点,
∴FD=2EG=2×4=8,EG=FG=4,
∴AD=AF+FD=2+8=10,
∵AG=AF+GF,
∴AG=2+4=6,
∴CD=AB=AG=6,
∵∠B=60°,
∴∠HDC=60°,
在Rt△AHC中,HD=![]() CD=3,
CD=3,
HC=![]() HD=3
HD=3![]() ,
,
∵AH=AD﹣HD=10﹣3=7,
在Rt△AHC中,AH2+HC2=AC2,
∴AC=![]() =
=![]() =2
=2![]() ;
;
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠ACB=∠DAC,
∵∠ACB=∠DCG,
∴∠DAC=∠DCG,
∵AB=AG,
∴CD=AG,
∵EG∥CD,
∴∠AGE=∠ADC,∠DCG=∠EGC,
在△AEG和△CGD中,
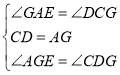
∴△AEG≌△CGD(ASA),
∴AE=CG,GE=DG,
∴∠GED=∠GDE,
∵EF⊥ED,
∴∠FED=90°,
∴∠GED+∠FEG=90°,
∴∠GDE+∠DFE=90°,
∴∠FEG=∠DFE,
又∠GCD=∠EGC=∠DAC,
在EG上截取GM=AF,连接CM,
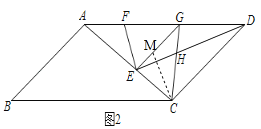
在△AFE和△GMC中,
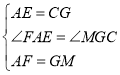 ,
,
∴△AFE≌△GMC(SAS),
∴∠AEF=∠GCM,∠AFE=∠GMC,
∴∠DFE=∠EMC,
∵∠FEG=∠DFE,
∴∠FEG=∠EMC,
∴FE∥CM,
∴∠AEF=∠ECM,
∴∠AEF=∠ECM=∠GCM,
∴∠ECG=∠ECM+∠GCM=2∠AEF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c过点A(3, 0)、点B(0, 3).点M(m, 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.
x2+bx+c过点A(3, 0)、点B(0, 3).点M(m, 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.
(1)求抛物线表达式;
(2)联结OP,当∠BOP=∠PBQ时,求PQ的长度;
(3)当△PBQ为等腰三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“3.15”植树节活动后,对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分:
栽下的各品种树苗棵数统计表 | ||||
植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
植树棵数 | 150 | 125 | 125 | |

若经观测计算得出丙种树苗的成活率为89.6%,请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共 棵,乙品种树苗 棵;
(2)图1中,甲 %、乙 %,并将图2补充完整;
(3)求这次植树活动的树苗成活率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一直线上有A、B两地,甲车从A地送货到B地,同时乙车从B地前往A地,两车皆匀速行驶.途中某一时刻,甲车发现有货物落在A、B之间的某处C地,于是立刻掉头并以自己原来速度的两倍匀速返回,取到货物后,再以最初的速度继续匀速向B地行驶.两车之间的距离y(千米)与甲车行驶的时间x(小时)之间的函数关系如图所示(途中掉头、取货物耽误时间忽略不计),当乙车到达A地时,甲车到A地的距离为_____千米.
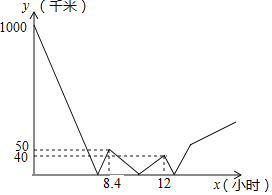
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,y是关于
,y是关于![]() 的二次函数,抛物线
的二次函数,抛物线![]() 经过点
经过点![]() .抛物线
.抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 则下列判断:
则下列判断:
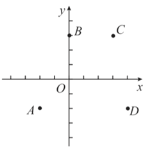
①四条抛物线的开口方向均向下;
②当![]() 时,四条抛物线表达式中的
时,四条抛物线表达式中的![]() 均随
均随![]() 的增大而增大;
的增大而增大;
③抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 顶点的上方;
顶点的上方;
④抛物线![]() 与
与![]() 轴交点在点
轴交点在点![]() 的上方.
的上方.
其中正确的是
A.①②④B.①③④
C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
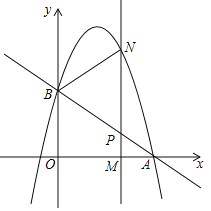
(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为线段OA上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
①试用含m的代数式表示线段PN的长;
②求线段PN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )

A.△OAB是等边三角形B.OC平分弦AB
C.∠BAC=30°D.弦AC的长等于圆内接正十二边形的边长
查看答案和解析>>
科目:初中数学 来源: 题型:
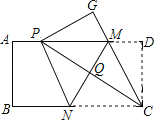
【题目】如图,先有一张矩形纸片![]() 点
点![]() 分别在矩形的边
分别在矩形的边![]() 上,将矩形纸片沿直线MN折叠,使点
上,将矩形纸片沿直线MN折叠,使点![]() 落在矩形的边
落在矩形的边![]() 上,记为点
上,记为点![]() ,点
,点![]() 落在
落在![]() 处,连接
处,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:
.下列结论:
![]()
②四边形![]() 是菱形;
是菱形;
③![]() 重合时,
重合时,![]() ;
;
④![]() 的面积
的面积![]() 的取值范围是
的取值范围是![]()
其中正确的是_____(把正确结论的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com