
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
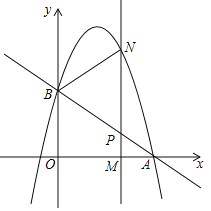
(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为线段OA上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
①试用含m的代数式表示线段PN的长;
②求线段PN的最大值.
【答案】(1)B(0,2),y=﹣![]() x2+
x2+![]() x+2;(2)①PN=﹣
x+2;(2)①PN=﹣![]() (0≤m≤3);②m=
(0≤m≤3);②m=![]() 时,线段PN有最大值为3.
时,线段PN有最大值为3.
【解析】
(1)把A点坐标代入直线解析式可求得c,则可求得B点坐标,由A、B的坐标,利用待定系数法可求得抛物线解析式;
(2)①M(m,0),则P(m,![]() ),N(m,﹣
),N(m,﹣![]() ),即可求出PN的长;
),即可求出PN的长;
②根据二次函数的性质可得线段PN的最大值.
解:(1)∵y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,
x+c与x轴交于点A(3,0),与y轴交于点B,
∴0=﹣2+c,解得c=2,
∴B(0,2),
∵抛物线y=﹣![]() x2+bx+c经过点A,B,
x2+bx+c经过点A,B,
∴![]() ,解得
,解得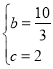 ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)①M(m,0),则P(m,![]() ),N(m,﹣
),N(m,﹣![]() ),
),
∴PN=![]() =﹣
=﹣![]() (0≤m≤3);
(0≤m≤3);
②∵PN=﹣![]() =
=![]() ,
,
∴m=![]() 时,线段PN有最大值为3.
时,线段PN有最大值为3.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了解初中学生参加综合实践活动的情况,随机抽取了本市初一、初二、初三年级各![]() 名学生进行了调查,调查结果如图所示,请你根据图中的信息回答问题.
名学生进行了调查,调查结果如图所示,请你根据图中的信息回答问题.
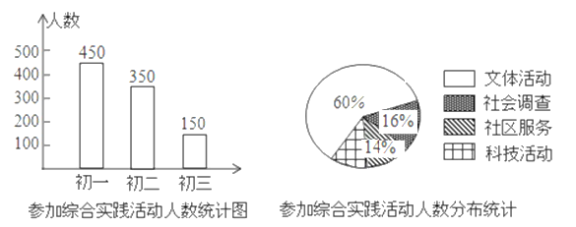
(1)在被调查的学生中,参加综合实践活动的有多少人,参加科技活动的有多少人;
(2)如果本市有![]() 万名初中学生,请你估计参加科技活动的学生约有多少名.
万名初中学生,请你估计参加科技活动的学生约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
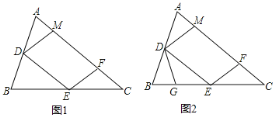
【题目】如图1,锐角△ABC中,D、E分别是AB、BC的中点,F是AC上的点,且∠AFE=∠A,DM//EF交AC于点M.
(1)求证:DM=DA;
(2)点G在BE上,且∠BDG=∠C,如图2,
① 求证:△DEG∽△ECF;
② 从线段CE上取一点H,连接FH使∠CFH=∠B,若BG=1,求EH的长.
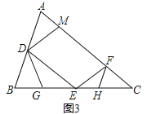
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E为对角线AC上一点,连接DE,作EF⊥DE,交AD于点F,G为AD边上一点,且AB=AG,连接GE.
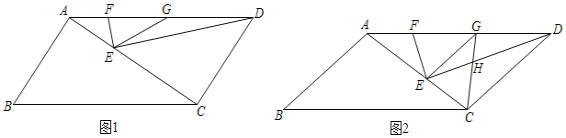
(1)如图1,若点G为DF的中点,AF=2,EG=4,∠B=60°,求AC的长;
(2)如图2,连接CG交DE于点H,若EG∥CD,∠ACB=∠DCG,求证:∠ECG=2∠AEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校今年组织学生参加志愿者活动,活动分为甲、乙、丙三组进行.下面的条形统计图和扇形统计图反映了学生参加活动的报名情况,请你根据图中的信息,解答下列问题:
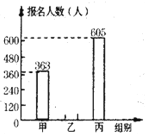
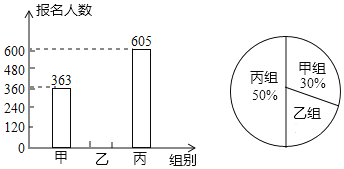
(1)若在参加活动的学生中随机抽取一名学生,则抽到乙组学生的概率是
(2)今年参加志愿者共 人,并把条形统计图补充完整;
(3)学校两年前参加志愿者的总人数是810人,若这两年的年增长率相同,求这个年增长率.(精确到1%)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
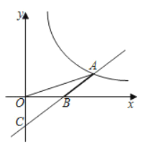
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为
为![]() 轴上一点,
轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
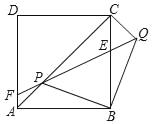
【题目】如图,正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上(点P与A、C不重合),QP与BC交于E,QP延长线与AD交于点F,连接CQ.
(1)①求证:AP=CQ;②求证:PA2=AFAD;
(2)若AP:PC=1:3,求tan∠CBQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF的长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为12,∠C=60°,则四边形ABEF的面积是( )
BF的长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为12,∠C=60°,则四边形ABEF的面积是( )

A.9![]() B.12C.
B.12C.![]() D.6
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com