
【题目】已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
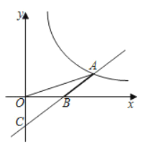
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为
为![]() 轴上一点,
轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
【答案】(1)反比例函数的表达式为![]() ,直线
,直线![]() 的表达式为
的表达式为![]() ;(2)
;(2)![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1) 过点![]() 作
作![]() 轴于
轴于![]() ,根据和
,根据和![]() 求出AD的长度,再利用
求出AD的长度,再利用![]() 和勾股定理得到BD的长度,进而得到答案;
和勾股定理得到BD的长度,进而得到答案;
(2)根据得到的![]() 是等腰三角形分情况
是等腰三角形分情况![]() 、
、![]() 、
、![]() 讨论即可得到答案;
讨论即可得到答案;
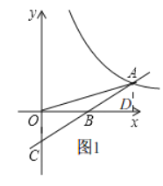
解:(1)如图,过点![]() 作
作![]() 轴于
轴于![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() (勾股定理),
(勾股定理),
∴![]() ,
,
∴![]() ,
,
将点![]() 坐标代入反比例函数
坐标代入反比例函数![]() 中得,
中得,![]() ,
,
∴反比例函数的表达式为![]() ,
,
将点![]() ,
,![]() 代入
代入![]() 中,
中,
得:![]() ,
,
解得: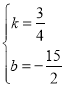
∴直线![]() 的表达式为
的表达式为![]()
(2)由(1)知,![]() ,
,
∵![]() 是等腰三角形,
是等腰三角形,
∴①当![]() 时,
时,
∴![]() ,
,
∴![]() 或
或![]() ,
,
②当![]() 时,如图:
时,如图:
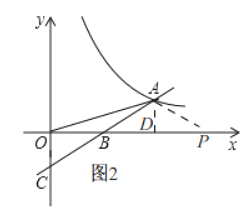
由(1)知,![]() ,
,
易知,点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
③当![]() 时,设
时,设![]() ,
,
∵![]() ,
,![]() ,
,
∴根据两点间的距离公式得到:![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
即:满足条件的点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】节假日期间向、某商场组织游戏,主持人请三位家长分别带自己的孩于参加游戏,A、B、C分别表示一位家长,他们的孩子分别对应的是a,b,![]() 若主持人分别从三位家长和三位孩予中各选一人参加游戏.
若主持人分别从三位家长和三位孩予中各选一人参加游戏.
![]() 若已选中家长A,则恰好选中自己孩子的概率是______.
若已选中家长A,则恰好选中自己孩子的概率是______.
![]() 请用画树状图或列表法求出被选中的恰好是同一家庭成员的概率.
请用画树状图或列表法求出被选中的恰好是同一家庭成员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“3.15”植树节活动后,对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分:
栽下的各品种树苗棵数统计表 | ||||
植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
植树棵数 | 150 | 125 | 125 | |

若经观测计算得出丙种树苗的成活率为89.6%,请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共 棵,乙品种树苗 棵;
(2)图1中,甲 %、乙 %,并将图2补充完整;
(3)求这次植树活动的树苗成活率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,y是关于
,y是关于![]() 的二次函数,抛物线
的二次函数,抛物线![]() 经过点
经过点![]() .抛物线
.抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 则下列判断:
则下列判断:
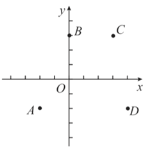
①四条抛物线的开口方向均向下;
②当![]() 时,四条抛物线表达式中的
时,四条抛物线表达式中的![]() 均随
均随![]() 的增大而增大;
的增大而增大;
③抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 顶点的上方;
顶点的上方;
④抛物线![]() 与
与![]() 轴交点在点
轴交点在点![]() 的上方.
的上方.
其中正确的是
A.①②④B.①③④
C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
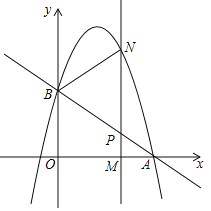
(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为线段OA上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
①试用含m的代数式表示线段PN的长;
②求线段PN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为 .
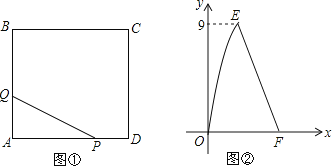
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )

A.△OAB是等边三角形B.OC平分弦AB
C.∠BAC=30°D.弦AC的长等于圆内接正十二边形的边长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】复课返校后,为了让同学们进一步了解“新型冠状病毒”的防控知识,某学校组织了一次关于“新型冠状病毒”的防控知识比赛,从问卷中随机抽查了一部分,对调查结果进行了分组统计,并制作了如下表格与条形统计图:
分组结果 | 频数 | 频率 |
A.完全掌握 | 30 | 0.3 |
B.比较清楚 | 50 |
|
C.不怎么清楚 |
| 0.15 |
D.不清楚 | 5 | 0.05 |
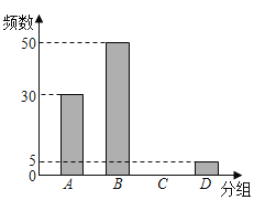
请根据上图完成下面题目:
(1)总人数为 人,![]() ,
,![]() ;
;
(2)请你补全条形统计图;
(3)若全校有2700人,请你估算一下全校对“新型冠状病毒”的防控知识“完全掌握”的人数有多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
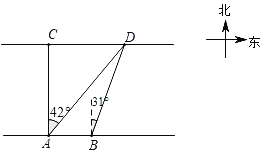
【题目】数学兴趣小组想测量河对岸两颗大树C、D之间的距离.如图所示,在河岸A点测得大树C位于正北方向上,大树D位于北偏东42°方向上.再沿河岸向东前进100米到达B处,测得大树D位于北偏东31°方向上.求两颗大树C、D之间的距离.(结果精确到1米.参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60,sin42°≈0.67,coo42°≈0.74,tan42°≈0.90).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com