
【题目】复课返校后,为了让同学们进一步了解“新型冠状病毒”的防控知识,某学校组织了一次关于“新型冠状病毒”的防控知识比赛,从问卷中随机抽查了一部分,对调查结果进行了分组统计,并制作了如下表格与条形统计图:
分组结果 | 频数 | 频率 |
A.完全掌握 | 30 | 0.3 |
B.比较清楚 | 50 |
|
C.不怎么清楚 |
| 0.15 |
D.不清楚 | 5 | 0.05 |
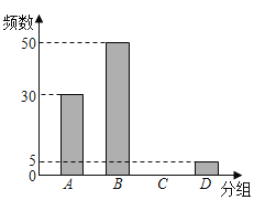
请根据上图完成下面题目:
(1)总人数为 人,![]() ,
,![]() ;
;
(2)请你补全条形统计图;
(3)若全校有2700人,请你估算一下全校对“新型冠状病毒”的防控知识“完全掌握”的人数有多少.
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
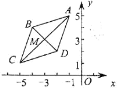
【题目】菱形ABCD在坐标平面内的位置如图所示,已知A(-1,5),D(-2,2),对角线交点M(-3,3),如果双曲线![]() (x<0)与菱形ABCD有公共点,那么k的取值范围是________
(x<0)与菱形ABCD有公共点,那么k的取值范围是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
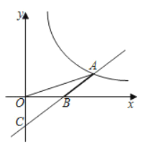
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为
为![]() 轴上一点,
轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某一广告墙PQ旁有两根直立的木杆AB和CD,某一时刻在太阳光下,木杆CD的影子刚好不落在广告墙PQ上.
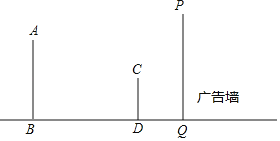
(1)画出太阳光线CE和AB的影子BF;
(2)若AB=10米,CD=6米,CD到PQ的距离DQ的长为8米,求此时木杆AB的影子BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
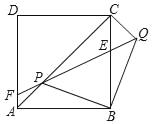
【题目】如图,正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上(点P与A、C不重合),QP与BC交于E,QP延长线与AD交于点F,连接CQ.
(1)①求证:AP=CQ;②求证:PA2=AFAD;
(2)若AP:PC=1:3,求tan∠CBQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P为△ABC边上一动点,沿着A→C→B的路径行进,点P作PD⊥AB,垂足为D,设AD=x,△APD的面积为y,图2是y关于x的函数图象,则依据图中的数量关系计算△ACB的周长为( )
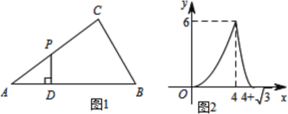

A.![]() B.15C.
B.15C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
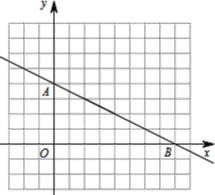
【题目】如图,单位长度为1的网格坐标系中,一次函数 ![]() 与坐标轴交于A、B两点,反比例函数
与坐标轴交于A、B两点,反比例函数![]() (x>0)经过一次函数上一点C(2,a).
(x>0)经过一次函数上一点C(2,a).
(1)求反比例函数解析式,并用平滑曲线描绘出反比例函数图像;
(2)依据图像直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
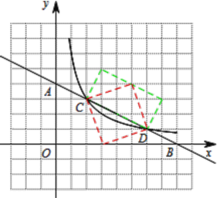
(3)若反比例函数![]() 与一次函数
与一次函数![]() 交于C、D两点,使用直尺与2B铅笔构造以C、D为顶点的矩形,且使得矩形的面积为10.
交于C、D两点,使用直尺与2B铅笔构造以C、D为顶点的矩形,且使得矩形的面积为10.
查看答案和解析>>
科目:初中数学 来源: 题型:
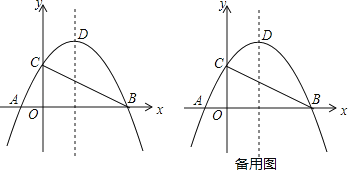
【题目】如图,抛物线y=﹣![]() x2+bx+c的图象经过点C,交x轴于点A(﹣1,0)、B(4,0)(A点在B点左侧),顶点为D.
x2+bx+c的图象经过点C,交x轴于点A(﹣1,0)、B(4,0)(A点在B点左侧),顶点为D.
(1)求抛物线的解析式;
(2)将△ABC沿直线BC对折,点A的对称点为A′,试求A′的坐标;
(3)抛物线的对称轴上是否存在点P,使∠BPC=∠BAC?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富综合实践活动,开设了四个实验室如下:A.物理;B.化学;C.信息;D.生物.为了解学生最喜欢哪个实验室,随机抽取了部分学生进行调查,每位被调查的学生都选择了一个自己最喜欢的实验室,调查后将调查结果绘制成了如图统计图,请根据统计图回答下列问题

(1)求这次被调查的学生人数.
(2)请将条形统计图补充完整.
(3)求出扇形统计图中B对应的圆心角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com