
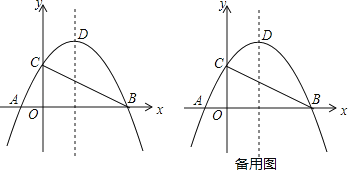
【题目】如图,抛物线y=﹣![]() x2+bx+c的图象经过点C,交x轴于点A(﹣1,0)、B(4,0)(A点在B点左侧),顶点为D.
x2+bx+c的图象经过点C,交x轴于点A(﹣1,0)、B(4,0)(A点在B点左侧),顶点为D.
(1)求抛物线的解析式;
(2)将△ABC沿直线BC对折,点A的对称点为A′,试求A′的坐标;
(3)抛物线的对称轴上是否存在点P,使∠BPC=∠BAC?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)A'(1,4);(3)存在,点P的坐标为(
x+2;(2)A'(1,4);(3)存在,点P的坐标为(![]() ,﹣
,﹣![]() )或(
)或(![]() ,2+
,2+![]() ).
).
【解析】
(1)先判断出抛物线的二次项系数,再根据交点式,即可得出结论;
(2)先判断出∠ACB=90°,进而得出AA'的中点恰好是点C,利用中点坐标公式即可得出结论;
(3)分点P在直线BC下方和上方,判断出点P在△ABC(或△A'BC的外接圆上,求出此圆的半径和圆心O'的坐标,即可得出结论.
解:(1)∵抛物线y=﹣![]() x2+bx+c交x轴于点A(﹣1,0)、B(4,0),
x2+bx+c交x轴于点A(﹣1,0)、B(4,0),
∴抛物线的解析式为y=﹣![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣![]() x2+
x2+![]() x+2,
x+2,
(2)如图,
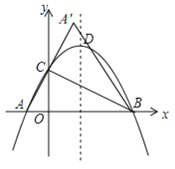
由(1)知,抛物线的解析式为y=﹣![]() x2+
x2+![]() x+2,
x+2,
则点C(0,2),
∵B(4,0),A(﹣1,0),
∴OA=1,OB=4,
∴![]() =
=![]() =
=![]() ,
,
∵∠AOC=∠COB=90°,
∴△AOC∽△COB,
∴∠ACO=∠CBO,
∵∠OCB+∠OBC=90°,
∴∠ACO+∠OCB=90°,
∴∠ACB=90°,
由折叠知,点A'与A关于BC对称,
则AA'与BC的交点恰为点C,
即点C是AA'的中点,
设点A(m,n),
则![]() =0,
=0,![]() =2,
=2,
∴m=1,n=4,
∴A'(1,4);
(3)如图,当点P在直线BC的下方时,

由(2)知,△ABC是以AB为斜边的直角三角形,
作Rt△ABC的外接圆,则圆心为抛物线与x轴的交点,记作O',
∴O'(![]() ,0),⊙O'半径为
,0),⊙O'半径为![]() ,
,
∴O'P=![]() ,设点P的坐标为(
,设点P的坐标为(![]() ,a),
,a),
∴O'P=﹣a,
∴﹣a=![]() ,
,
∴a=﹣![]() ,
,
∴P(![]() ,﹣
,﹣![]() );
);
如图,当点P在直线BC上方时,
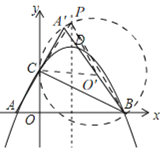
由(2)知,A'(1,4),
由折叠知,△A'BC是以A'B为斜边的直角三角形,作Rt△A'BC的外接圆,记圆心为O',O'是A'B的中点,
∵B(4,0),
∴O'(![]() ,2),⊙O'的半径为
,2),⊙O'的半径为![]() ,
,
∵∠BPC=∠BAC,
∴点P在⊙O'上,
∴O'P=![]()
设点P(![]() ,d)(d>1),
,d)(d>1),
∴O'P=![]() =
=![]()
∴d=2﹣![]() (舍)或d=2+
(舍)或d=2+![]() ,
,
∴P(![]() ,2+
,2+![]() ),
),
即满足条件的点P的坐标为(![]() ,﹣
,﹣![]() )或(
)或(![]() ,2+
,2+![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,y是关于
,y是关于![]() 的二次函数,抛物线
的二次函数,抛物线![]() 经过点
经过点![]() .抛物线
.抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 则下列判断:
则下列判断:
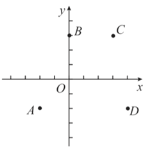
①四条抛物线的开口方向均向下;
②当![]() 时,四条抛物线表达式中的
时,四条抛物线表达式中的![]() 均随
均随![]() 的增大而增大;
的增大而增大;
③抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 顶点的上方;
顶点的上方;
④抛物线![]() 与
与![]() 轴交点在点
轴交点在点![]() 的上方.
的上方.
其中正确的是
A.①②④B.①③④
C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】复课返校后,为了让同学们进一步了解“新型冠状病毒”的防控知识,某学校组织了一次关于“新型冠状病毒”的防控知识比赛,从问卷中随机抽查了一部分,对调查结果进行了分组统计,并制作了如下表格与条形统计图:
分组结果 | 频数 | 频率 |
A.完全掌握 | 30 | 0.3 |
B.比较清楚 | 50 |
|
C.不怎么清楚 |
| 0.15 |
D.不清楚 | 5 | 0.05 |
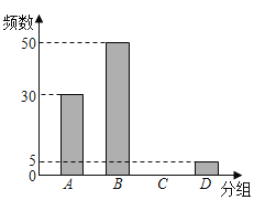
请根据上图完成下面题目:
(1)总人数为 人,![]() ,
,![]() ;
;
(2)请你补全条形统计图;
(3)若全校有2700人,请你估算一下全校对“新型冠状病毒”的防控知识“完全掌握”的人数有多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间是一次函数关系.如图所示是一个家用温度表的表盘、其左边为摄氏温度的刻度和读数(单位![]() ),右边为华氏温度的刻度和读数(单位
),右边为华氏温度的刻度和读数(单位![]() ).从温度计的刻度上可以看出,摄氏温度
).从温度计的刻度上可以看出,摄氏温度![]() 与华氏温度
与华氏温度![]() 部分对应关系如下表:
部分对应关系如下表:
| ··· |
|
| ··· |
| ··· |
|
| ··· |

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当摄氏温度为零下![]() 时,求华氏温度为多少?
时,求华氏温度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,先有一张矩形纸片![]() 点
点![]() 分别在矩形的边
分别在矩形的边![]() 上,将矩形纸片沿直线MN折叠,使点
上,将矩形纸片沿直线MN折叠,使点![]() 落在矩形的边
落在矩形的边![]() 上,记为点
上,记为点![]() ,点
,点![]() 落在
落在![]() 处,连接
处,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:
.下列结论:
![]()
②四边形![]() 是菱形;
是菱形;
③![]() 重合时,
重合时,![]() ;
;
④![]() 的面积
的面积![]() 的取值范围是
的取值范围是![]()
其中正确的是_____(把正确结论的序号都填上).
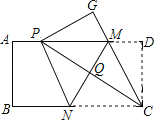
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 直径,以
直径,以![]() 为边作等腰
为边作等腰![]() ,且
,且![]() ,
,![]() 与边
与边![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,并交
,并交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)若![]() ,
,![]() °,求由线段
°,求由线段![]() 、
、![]() 及
及![]() 所围成的图形(阴影部分)面积.
所围成的图形(阴影部分)面积.
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组想测量河对岸两颗大树C、D之间的距离.如图所示,在河岸A点测得大树C位于正北方向上,大树D位于北偏东42°方向上.再沿河岸向东前进100米到达B处,测得大树D位于北偏东31°方向上.求两颗大树C、D之间的距离.(结果精确到1米.参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60,sin42°≈0.67,coo42°≈0.74,tan42°≈0.90).
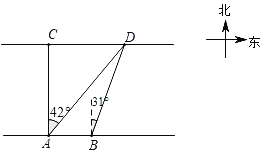
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮分别从同一直线跑道A、B两端同时相向匀速出发,第一次相遇后小明觉得自己速度太慢便立即提速至原速的1.5倍,然后匀速运动到B端,且小明到达B端后立即以提速后的速度调头返回.小亮匀速跑步到A端后,立即按原速返回(忽略小明、小亮调头时间),当小明、小亮再次相遇时二人停止运动.已知两人相距的距离y(米)与小亮出发时间x(秒)之间的关系如图所示,则第二次相遇时小明与B端的距离为______米.
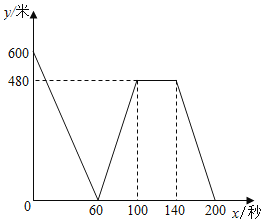
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着宁波市江北区慈城古县城旅游开发的推进,到慈城旅游的全国各地游客逐年上升.深受当地老百姓喜爱的两种本土特产杨梅和年糕,也深受外地游客的青睐.现在,有两种特产大礼包的组合是这样的:若购买2筐杨梅和3盒年糕,则需花费270元;若购买1筐杨梅和4盒年糕,则需花费260元.(杨梅、年糕分别按包装筐和包装盒计价)
(1)求一筐杨梅、一盒年糕的售价分别是多少元?
(2)如果需购买两种特产共12件(1筐或1盒称为1件),要求年糕的盒数不高于杨梅筐数的两倍,请你设计一种购买方案,使所需总费用最低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com