练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】节假日期间向、某商场组织游戏，主持人请三位家长分别带自己的孩于参加游戏，A、B、C分别表示一位家长，他们的孩子分别对应的是a，b，若主持人分别从三位家长和三位孩予中各选一人参加游戏．

    若已选中家长A，则恰好选中自己孩子的概率是______．

    请用画树状图或列表法求出被选中的恰好是同一家庭成员的概率．

    【答案】（1）；（2）.

    【解析】

    （1）根据概率公式直接得出答案即可；

    （2）先画出树状图，得出所有等情况数和恰好是同一家庭成员的情况数，然后根据概率公式即可得出答案．

    解：有三位孩子，分别是a，b，c，

    家长A恰好选中自己孩子的概率是；

    故答案为：．

    画树状图如下：

    共有9种等情况数，恰好是同一家庭成员的有3种情况数，

    被选中的恰好是同一家庭成员的概率是．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

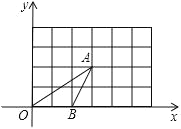
    【题目】如图，△OAB的顶点坐标分别为O（0，0）、A（3，2）、B（2，0），将这三个顶点的坐标同时扩大到原来的2倍，得到对应点D、E、F．

    (1)在图中画出△DEF；

    (2)点E是否在直线OA上？为什么？

    (3)△OAB与△DEF______位似图形（填“是”或“不是”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在△ABC中，以AC为边在△ABC外作等边△ACD，BC=，AD=，tan∠ACB=，则线段BD的长为_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在每个小正方形的边长为 1 的网格中，点 A、B、C 均在格点上，BC 与网格交于点 P，（1）△ABC 的面积等于______；（2）在 AC 边上有一点 Q，当 PQ 平分△ABC 的面积时，请在如图所示的网格中，用无刻度的直尺，画出 PQ，并简要说明点 Q 的位置是如何找到的(不要求证明)_____________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共4个，某学习小组进行摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再放回，下表是活动进行中的一组统计数据：

    摸球的次数n

    100

    150

    200

    500

    800

    1000

    摸到黑球的次数m

    23

    33

    60

    130

    202

    251

    摸到黑球的频率

    当n很大时，估计从袋中摸出一个黑球的概率是______；

    试估算口袋中白球有______个；

    在的条件下，若从中先换出一球，不放回，摇匀后再摸出一球，请用列表或树状图的方法求两次都摸到白球的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一租赁公司拥有某种型号的汽车10辆，公司在经营中发现每辆汽车每天的租赁价为120元时可全部出租，租赁价每涨3元就少出租1辆，公司决定采取涨价措施．

    填空：每天租出的汽车数辆与每辆汽车的租赁价元之间的关系式为______．

    已知租出的汽车每辆每天需要维护费30元，求租出汽车每天的实际收入元与每辆汽车的租赁价元之间的关系式；租出汽车每天的实际收入租出收入租出汽车维护费

    若未租出的汽车每辆每天需要维护费12元，则每辆汽车每天的租赁价元定为多少元时，才能使公司获得日收益元最大？并求出公司的最大日收益．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

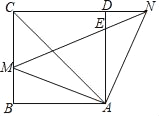
    【题目】如图，在正方形ABCD中，点M是边BC上的一点（不与B、C重合），点N在CD边的延长线上，且满足∠MAN=90°，联结MN、AC，N与边AD交于点E．

    （1）求证：AM=AN；

    （2）如果∠CAD=2∠NAD，求证：AM2=ACAE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明与同学们在数学动手实践操作活动中，将锐角为的直角三角板MPN的一个锐角顶点P与正方形ABCD的顶点A重合，正方形ABCD固定不动，然后将三角板绕着点A旋转，的两边分别与正方形的边BC、DC或其延长线相交于点E、F，连结EF．

    （探究发现）

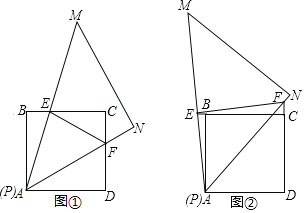
    在三角板旋转过程中，当的两边分别与正方形的边CB、DC相交时，如图所示，请直接写出线段BE、DF、EF满足的数量关系：______．

    （拓展思考）

    在三角板旋转过程中，当的两边分别与正方形的边CB、DC的延长线相交时，如图所示，则线段BE、DF、EF又将满足怎样的数量关系：______，并证明你的结论；

    （创新应用）

    若正方形的边长为4，在三角板旋转过程中，当的一边恰好经过BC边的中点时，试求线段EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（探索发现）

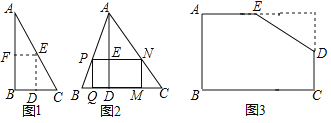
    如图1，是一张直角三角形纸片，，小明想从中剪出一个以为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE、EF剪下时，所得的矩形的面积最大，随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为______．

    （拓展应用）

    如图2，在中，，BC边上的高，矩形PQMN的顶点P、N分别在边AB、AC上，顶点Q、M在边BC上，求出矩形PQMN面积的最大值用含a、h的代数式表示；

    （灵活应用）

    如图3，有一块“缺角矩形”ABCDE，，，，，小明从中剪出了一个面积最大的矩形为所剪出矩形的内角，直接写出该矩形的面积．

    查看答案和解析>>

    同步练习册答案