
【题目】一租赁公司拥有某种型号的汽车10辆,公司在经营中发现每辆汽车每天的租赁价为120元时可全部出租,租赁价每涨3元就少出租1辆,公司决定采取涨价措施.
![]() 填空:每天租出的汽车数
填空:每天租出的汽车数![]() 辆
辆![]() 与每辆汽车的租赁价
与每辆汽车的租赁价![]() 元
元![]() 之间的关系式为______.
之间的关系式为______.
![]() 已知租出的汽车每辆每天需要维护费30元,求租出汽车每天的实际收入
已知租出的汽车每辆每天需要维护费30元,求租出汽车每天的实际收入![]() 元
元![]() 与每辆汽车的租赁价
与每辆汽车的租赁价![]() 元
元![]() 之间的关系式;
之间的关系式;![]() 租出汽车每天的实际收入
租出汽车每天的实际收入![]() 租出收入
租出收入![]() 租出汽车维护费
租出汽车维护费![]()
![]() 若未租出的汽车每辆每天需要维护费12元,则每辆汽车每天的租赁价
若未租出的汽车每辆每天需要维护费12元,则每辆汽车每天的租赁价![]() 元
元![]() 定为多少元时,才能使公司获得日收益
定为多少元时,才能使公司获得日收益![]() 元
元![]() 最大?并求出公司的最大日收益.
最大?并求出公司的最大日收益.
【答案】(1)![]() (2)
(2)![]() ;(3)将每辆汽车的日租金定为120元,才能使公司获得最大日收益,公司的最大日收益是900元.
;(3)将每辆汽车的日租金定为120元,才能使公司获得最大日收益,公司的最大日收益是900元.
【解析】
(1)判断出y与x的函数关系为一次函数关系,再根据待定系数法求出函数解析式;
(2)根据租出汽车每天的实际收入=租出收入﹣租出汽车维护费即可得到结论;
(3)租出的车的利润减去未租出车的维护费,即为公司月收益,再利用二次函数的性质求解可得.
解:![]() 根据题意得,y与x满足一次函数关系,设
根据题意得,y与x满足一次函数关系,设![]() ,
,
则![]() ,
,
解得: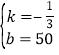 ,
,
即每天租出的汽车数![]() 辆
辆![]() 与每辆汽车的租赁价
与每辆汽车的租赁价![]() 元
元![]() 之间的关系式为:
之间的关系式为:![]() ;
;
故答案为:![]() ;
;
![]() 设公司获得的日收益为w,
设公司获得的日收益为w,
则![]()
![]() ;
;
![]() ,
,
![]() 当
当![]() 时,z随x的增大而减小,
时,z随x的增大而减小,
![]() 当
当![]() 时,z取得最大值,最大值
时,z取得最大值,最大值![]() ,
,
答:将每辆汽车的日租金定为120元,才能使公司获得最大日收益,公司的最大日收益是900元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
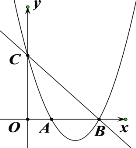
【题目】如图,在平面直角坐标系中,抛物线![]() 交x轴正半轴于点A、点B,交y轴于点C, 直线y=-x+6经过点B、点C;
交x轴正半轴于点A、点B,交y轴于点C, 直线y=-x+6经过点B、点C;
(1)求抛物线的解析式 ;
(2)点D在x轴下方的抛物线上,连接DB、DC,点D的横坐标为t,△BCD的面积为S,求S与t的函数关系式,并直接写出自变量t的取值范围 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
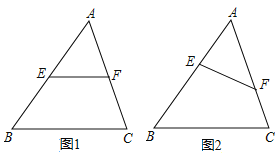
【题目】在△ABC 中,E、F 分别为线段 AB、AC 上的点(不与 A、B、C 重合)
(1)如图 1,若 EF//BC,求证:![]()
(2)如图 2,若 EF 不与 BC 平行,(1)中的结论是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节假日期间向、某商场组织游戏,主持人请三位家长分别带自己的孩于参加游戏,A、B、C分别表示一位家长,他们的孩子分别对应的是a,b,![]() 若主持人分别从三位家长和三位孩予中各选一人参加游戏.
若主持人分别从三位家长和三位孩予中各选一人参加游戏.
![]() 若已选中家长A,则恰好选中自己孩子的概率是______.
若已选中家长A,则恰好选中自己孩子的概率是______.
![]() 请用画树状图或列表法求出被选中的恰好是同一家庭成员的概率.
请用画树状图或列表法求出被选中的恰好是同一家庭成员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票原定的票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出200件![]() 如每件商品的售价每上涨1元,则每个月少卖5件
如每件商品的售价每上涨1元,则每个月少卖5件![]() 设每件商品的售价上涨x元,每个月销售利润为y元.
设每件商品的售价上涨x元,每个月销售利润为y元.
![]() 求y与x的函数关系式;
求y与x的函数关系式;
![]() 每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
![]() 每件商品的售价定在什么范围时,每个月的利润不低于3000元?
每件商品的售价定在什么范围时,每个月的利润不低于3000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com