
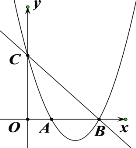
【题目】如图,在平面直角坐标系中,抛物线![]() 交x轴正半轴于点A、点B,交y轴于点C, 直线y=-x+6经过点B、点C;
交x轴正半轴于点A、点B,交y轴于点C, 直线y=-x+6经过点B、点C;
(1)求抛物线的解析式 ;
(2)点D在x轴下方的抛物线上,连接DB、DC,点D的横坐标为t,△BCD的面积为S,求S与t的函数关系式,并直接写出自变量t的取值范围 ;
【答案】(1)y=![]() ;(2)S=
;(2)S=![]() (2<t<6).
(2<t<6).
【解析】
(1)先根据一次函数y=-x+6求出B、C的坐标,再代入二次函数![]() 即可求出b,c的值;(2)设D点在抛物线AB之间,连接CD交x轴与H,设直线CD为y=kx+6,把点D求得k=
即可求出b,c的值;(2)设D点在抛物线AB之间,连接CD交x轴与H,设直线CD为y=kx+6,把点D求得k=![]() ,故y=
,故y=![]() x+6,令y=0求出H(
x+6,令y=0求出H(![]() ,0),再根据S△BCD=S△BDH+S△BHC=
,0),再根据S△BCD=S△BDH+S△BHC=![]() 即可进行求解化简.
即可进行求解化简.
(1)对于直线y=-x+6经过点B、点C,
令x=0,得y=6,即C(0,6)
令y=0,得x=6,即B(6,0)
把B(6,0),C(0,6)代入![]() ,得b=-4,c=6,
,得b=-4,c=6,
∴抛物线的解析式y=![]() ;
;
(2)令y=![]() =0,求得x1=2,x2=6,
=0,求得x1=2,x2=6,
∴A(2,0)
D点在抛物线AB之间,连接CD交x轴与H,设D(t,![]() )故2<t<6
)故2<t<6
设直线CD为y=kx+6
把点D代入得![]() =kx+6
=kx+6
得k=![]() ,
,
∴y=![]() x+6,
x+6,
令y=![]() x+6=0,得x=
x+6=0,得x=![]()
∴H(![]() ,0)
,0)
故S△BCD=S△BDH+S△BHC=![]() =
=![]() =
=![]() =
=![]() (2<t<6)
(2<t<6)


科目:初中数学 来源: 题型:
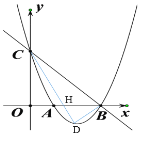
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0,其中正确的命题是( )
A. ①②③B. ①③C. ①④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
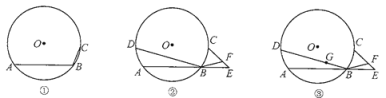
【题目】问题1如图①点A、B、C在⊙O上,且∠ABC=120°,⊙O的半径是3.求弧AC的长.
问题2如图②点A、B、C、D在⊙![]() 上,且弧AD=弧BC,E是AB的延长线上的
上,且弧AD=弧BC,E是AB的延长线上的![]() .
.
(1)设BD=nBF,则n=________;
(2)如图③若G是线段BD上的一个点,且![]() .试探究,在⊙
.试探究,在⊙![]() 上是否存在点P (B除外)使PG=PF?为什么?
上是否存在点P (B除外)使PG=PF?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
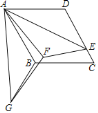
【题目】如图,在菱形ABCD中,![]() ,点E在边CD上,且
,点E在边CD上,且![]() ,
,![]() 与
与![]() 关于AE所在的直线成对称图形
关于AE所在的直线成对称图形![]() 以点A为中心,把
以点A为中心,把![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,连接GF,则线段GF的长为______.
,连接GF,则线段GF的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
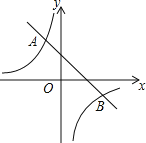
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象分别交于第二、四象限的A,B两点,点A的横坐标为
的图象分别交于第二、四象限的A,B两点,点A的横坐标为![]() .
.
![]() 求反比例函数的表达式;
求反比例函数的表达式;
![]() 根据图象回答:当x取何值时,
根据图象回答:当x取何值时,![]() 请直接写出答案:______.
请直接写出答案:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为 1 的网格中,点 A、B、C 均在格点上,BC 与网格交于点 P,(1)△ABC 的面积等于______;(2)在 AC 边上有一点 Q,当 PQ 平分△ABC 的面积时,请在如图所示的网格中,用无刻度的直尺,画出 PQ,并简要说明点 Q 的位置是如何找到的(不要求证明)_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一租赁公司拥有某种型号的汽车10辆,公司在经营中发现每辆汽车每天的租赁价为120元时可全部出租,租赁价每涨3元就少出租1辆,公司决定采取涨价措施.
![]() 填空:每天租出的汽车数
填空:每天租出的汽车数![]() 辆
辆![]() 与每辆汽车的租赁价
与每辆汽车的租赁价![]() 元
元![]() 之间的关系式为______.
之间的关系式为______.
![]() 已知租出的汽车每辆每天需要维护费30元,求租出汽车每天的实际收入
已知租出的汽车每辆每天需要维护费30元,求租出汽车每天的实际收入![]() 元
元![]() 与每辆汽车的租赁价
与每辆汽车的租赁价![]() 元
元![]() 之间的关系式;
之间的关系式;![]() 租出汽车每天的实际收入
租出汽车每天的实际收入![]() 租出收入
租出收入![]() 租出汽车维护费
租出汽车维护费![]()
![]() 若未租出的汽车每辆每天需要维护费12元,则每辆汽车每天的租赁价
若未租出的汽车每辆每天需要维护费12元,则每辆汽车每天的租赁价![]() 元
元![]() 定为多少元时,才能使公司获得日收益
定为多少元时,才能使公司获得日收益![]() 元
元![]() 最大?并求出公司的最大日收益.
最大?并求出公司的最大日收益.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为x,两人之间的距离为y,则下列选项中的图象能大致反映y与x之间关系的是( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com