
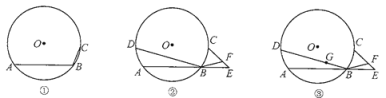
【题目】问题1如图①点A、B、C在⊙O上,且∠ABC=120°,⊙O的半径是3.求弧AC的长.
问题2如图②点A、B、C、D在⊙![]() 上,且弧AD=弧BC,E是AB的延长线上的
上,且弧AD=弧BC,E是AB的延长线上的![]() .
.
(1)设BD=nBF,则n=________;
(2)如图③若G是线段BD上的一个点,且![]() .试探究,在⊙
.试探究,在⊙![]() 上是否存在点P (B除外)使PG=PF?为什么?
上是否存在点P (B除外)使PG=PF?为什么?
【答案】问题1:![]() ;问题2:(1)
;问题2:(1)![]() ;(1)详见解析
;(1)详见解析
【解析】
问题一:根据弧长的计算公式,根据∠ABC=120°,找到∠AOC的度数,再由弧长公式计算出弧AC的长即可;
问题二:(1)连接AC,易证AC=3BF,然后再证明AC=BD,可得到n的值;
(2) 由(1)可证BG=BF,过点B作AE的垂线,与圆的交点即是点P.
问题一:解:如图,连接OA和OC
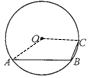
∵∠ABC=120°
∴∠AOC=360°-2∠ABC=120°
∴![]() =
=![]() =
=![]()
问题2:解:(1)如图,连接AC
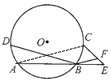
∵弧AD=弧BC
∴弧BD=弧AC
∴BD=AC
∵![]()
∴![]() ,∠BEF=∠AEC
,∠BEF=∠AEC
∴△BEF∽△AEC
∴![]()
∴![]() ,即3BF=BD
,即3BF=BD
∴n=3
(2) 如图,连接GF,过点B作AE的垂线,与GF交于点H,与圆的交点即是点P
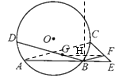
由(1)得△BEF∽△AEC,![]()
∵![]()
∴BF=BG
∴△BGF为等腰三角形
∴∠FBE=∠CAE
∵弧AD=弧BC
∴∠ABD=∠CAB
∴∠DBA=∠FBE
∵∠ABH=∠EBH=90°
∴∠DBH=∠FBH
∴BH为GF的中垂线
∴PG=PF
故存在P.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究同一坐标系中系数互为倒数的正、反比例函数![]() 与
与![]() 的图象性质
的图象性质![]() 小明根据学习函数的经验,对这两个函数当
小明根据学习函数的经验,对这两个函数当![]() 时的图象性质进行了探究
时的图象性质进行了探究![]() 设函数
设函数![]() 与
与![]() 图象的交点为A、
图象的交点为A、![]() 下面是小明的探究过程:
下面是小明的探究过程:
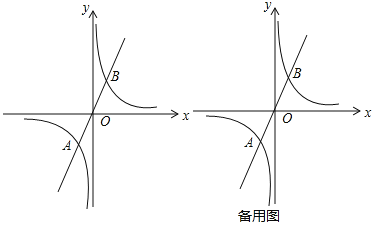
(1)如图所示,若已知A的坐标为![]() ,则B点的坐标为______.
,则B点的坐标为______.
(2)若A的坐标为![]() ,P点为第一象限内双曲线上不同于点B的任意一点.
,P点为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M,直线PB交x轴于点![]() 求证:
求证:![]() .
.
证明过程如下:设![]() ,直线PA的解析式为
,直线PA的解析式为![]() .
.
则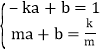
解得![]()
所以,直线PA的解析式为______.
请把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为![]() 时,判断
时,判断![]() 的形状,并用k表示出
的形状,并用k表示出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形![]() 中,
中, ![]() ,垂足为
,垂足为![]() 与
与![]() 的延长线相交于
的延长线相交于![]() ,且
,且![]() ,连接
,连接![]() ;
;
(1)如图![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
(2)如图![]() ,连接
,连接![]() ,若
,若![]() ,在不添加任何辅助线的情况下,直接写出图
,在不添加任何辅助线的情况下,直接写出图![]() 中所有面积等于
中所有面积等于![]() 的面积的钝角三角形.
的面积的钝角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
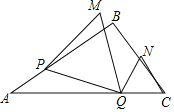
【题目】如图,在△ABC中,AB=7.5,AC=9,S△ABC=![]() .动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.
.动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.
(1)求cosA的值;
(2)当△PQM与△QCN的面积满足S△PQM=![]() S△QCN时,求t的值;
S△QCN时,求t的值;
(3)当t为何值时,△PQM的某个顶点(Q点除外)落在△QCN的边上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近期末考试,心理专家建议考生可通过以下四种方式进行考前减压:![]() .享受美食,
.享受美食,![]() .交流谈心,
.交流谈心,![]() .体育锻炼,
.体育锻炼,![]() .欣赏艺术.
.欣赏艺术.
(1)随机采访一名九年级考生,选择其中某一种方式,他选择“享受美食”的概率是 .
(2)同时采访两名九年级考生,请用画树状图或列表的方法求他们中至少有一人选择“欣赏艺术”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于反比例函数y=![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 函数图象分别位于第一、第三象限
B. 当x>0时,y随x的增大而减小
C. 函数图象经过点(1,2)
D. 若点A(x1,y1),B(x2,y2)都在函数图象上,且x1<x2,则y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
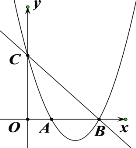
【题目】如图,在平面直角坐标系中,抛物线![]() 交x轴正半轴于点A、点B,交y轴于点C, 直线y=-x+6经过点B、点C;
交x轴正半轴于点A、点B,交y轴于点C, 直线y=-x+6经过点B、点C;
(1)求抛物线的解析式 ;
(2)点D在x轴下方的抛物线上,连接DB、DC,点D的横坐标为t,△BCD的面积为S,求S与t的函数关系式,并直接写出自变量t的取值范围 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票原定的票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com