【题目】临近期末考试，心理专家建议考生可通过以下四种方式进行考前减压：
.享受美食，
.交流谈心，
.体育锻炼，
.欣赏艺术.
（1）随机采访一名九年级考生，选择其中某一种方式，他选择“享受美食”的概率是 ．
（2）同时采访两名九年级考生，请用画树状图或列表的方法求他们中至少有一人选择“欣赏艺术”的概率.
阅读快车系列答案科目：初中数学 来源： 题型：
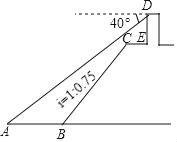
【题目】如图，小王在长江边某瞭望台D处测得江面上的渔船A的俯角为40°，若DE＝3米，CE＝2米，CE平行于江面AB，迎水坡BC的坡度i＝1：0.75，坡长BC＝10米，则此时AB的长约为多少米？（结果精确到0.1，参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）
查看答案和解析>>
科目：初中数学 来源： 题型：
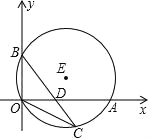
【题目】如图，直径为13的⊙E，经过原点O，并且与x轴、y轴分别交于A、B两点，线段OA、OB(OA＞OB)的长分别是方程x2+kx+60＝0的两根．
(1)OA：OB＝____；
(2)若点C在劣弧OA上，连结BC交OA于D，当△BOC∽△BDA时，点D的坐标为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
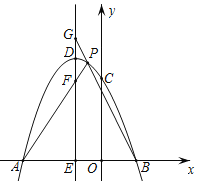
【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A、B两点（A在B的左侧），且OA=3，OB=1，与y轴交于C（0，3），抛物线的顶点坐标为D（﹣1，4）．
（1）求A、B两点的坐标；
（2）求抛物线的解析式；
（3）过点D作直线DE∥y轴，交x轴于点E，点P是抛物线上B、D两点间的一个动点（点P不与B、D两点重合），PA、PB与直线DE分别交于点F、G，当点P运动时，EF+EG是否为定值？若是，试求出该定值；若不是，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
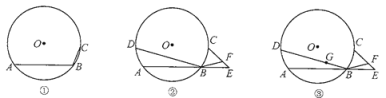
【题目】问题1如图①点A、B、C在⊙O上，且∠ABC=120°，⊙O的半径是3.求弧AC的长.
问题2如图②点A、B、C、D在⊙
上，且弧AD=弧BC，E是AB的延长线上的
.
(1)设BD=nBF，则n=________;
(2)如图③若G是线段BD上的一个点，且
.试探究，在⊙上是否存在点P (B除外)使PG=PF?为什么?
查看答案和解析>>
科目：初中数学 来源： 题型：
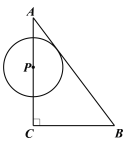
【题目】如图，
中，
，
，
.点
从点
出发，沿着
运动，速度为
个单位/
，在点运动的过程中，以为圆心的圆始终与斜边
相切,设⊙的面积为
，点的运动时间为
（）（
）.
（1）当
时，
；（用含的式子表示）
（2）求与的函数表达式；
（3）在⊙P运动过程中，当⊙P与三角形ABC的另一边也相切时，直接写出t的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
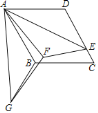
【题目】如图，在菱形ABCD中，
，点E在边CD上，且
，
与
关于AE所在的直线成对称图形
以点A为中心，把
顺时针旋转
，得到
，连接GF，则线段GF的长为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
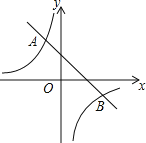
【题目】如图，一次函数
的图象与反比例函数
的图象分别交于第二、四象限的A，B两点，点A的横坐标为
．
求反比例函数的表达式；
根据图象回答：当x取何值时，
请直接写出答案：______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲骑自行车、乙骑摩托车沿相同路线由A地到B地，行驶过程中路程与时间的函数关系的图象如图. 根据图象解决下列问题：
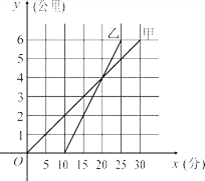
(1) 谁先出发？先出发多少时间？谁先到达终点？先到多少时间？
(2) 分别求出甲、乙两人的行驶速度；
(3) 在什么时间段内，两人均行驶在途中(不包括起点和终点)？在这一时间段内，请你根据下列情形，分别列出关于行驶时间x的方程或不等式(不化简，也不求解)：① 甲在乙的前面；② 甲与乙相遇；③ 甲在乙后面.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
