
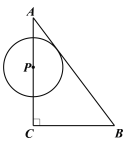
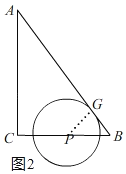
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 运动,速度为
运动,速度为![]() 个单位/
个单位/![]() ,在点
,在点![]() 运动的过程中,以
运动的过程中,以![]() 为圆心的圆始终与斜边
为圆心的圆始终与斜边![]() 相切,设⊙
相切,设⊙![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() (
(![]() )(
)(![]() ).
).
(1)当![]() 时,
时,![]() ;(用含
;(用含![]() 的式子表示)
的式子表示)
(2)求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)在⊙P运动过程中,当⊙P与三角形ABC的另一边也相切时,直接写出t的值.
【答案】(1)7-t(2)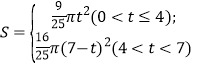 (3)
(3)![]()
【解析】
(1)先判断出点P在BC上,即可得出结论;
(2)分点P在边AC和BC上两种情况:利用相似三角形的性质得出比例式建立方程求解即可得出结论;
(3)分点P在边AC和BC上两种情况:借助(2)求出的圆P的半径等于PC,建立方程求解即可得出结论.
(1)∵AC=4,BC=3,∴AC+BC=7.
∵4<t<7,∴点P在边BC上,∴BP=7﹣t.
故答案为:7﹣t;
(2)在Rt△ABC中,AC=4,BC=3,根据勾股定理得:AB=5,由运动知,AP=t,分两种情况讨论:
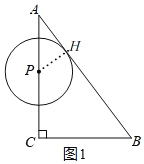
①当点P在边AC上时,即:0<t≤4,如图1,记⊙P与边AB的切点为H,连接PH,∴∠AHP=90°=∠ACB.
∵∠A=∠A,∴△APH∽△ACB,∴![]() ,∴
,∴![]() ,∴PH
,∴PH![]() t,∴S
t,∴S![]() πt2;
πt2;
②当点P在边BC上时,即:4<t<7,如图,记⊙P与边AB的切点为G,连接PG,∴∠BGP=90°=∠C.
∵∠B=∠B,∴△BGP∽△BCA,∴![]() ,∴
,∴![]() ,∴PG
,∴PG![]() (7﹣t),∴S
(7﹣t),∴S![]() π(7﹣t)2.
π(7﹣t)2.
综上所述:S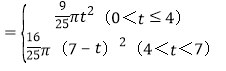 ;
;
(3)分两种情况讨论:
①当点P在边AC上时,即:0<t≤4,由(2)知,⊙P的半径PH![]() t.
t.
∵⊙P与△ABC的另一边相切,即:⊙P和边BC相切,∴PC=PH.
∵PC=4﹣t,∴4﹣t![]() t,∴t
t,∴t![]() 秒;
秒;
②当点P在边BC上时,即:4<t<7,由(2)知,⊙P的半径PG![]() (7﹣t).
(7﹣t).
∵⊙P与△ABC的另一边相切,即:⊙P和边AC相切,∴PC=PG.
∵PC=t﹣4,∴t﹣4![]() (7﹣t),∴t
(7﹣t),∴t![]() 秒.
秒.
综上所述:在⊙P运动过程中,当⊙P与三角形ABC的另一边也相切时,t的值为![]() 秒或
秒或![]() 秒.
秒.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
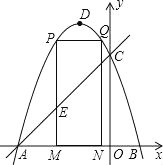
【题目】如图,抛物线y=﹣x2﹣2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM.如图,点P在点Q左边,试用含m的式子表示矩形PQNM的周长;
(3)当矩形PQNM的周长最大时,m的值是多少?并求出此时的△AEM的面积;
(4)在(3)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=2![]() DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区2015年投入教育经费2900万元,2017年投入教育经费3509万元.
(1)求2015年至2017年该地区投入教育经费的年平均增长率;
(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的增长情况,该地区到2019年需投入教育经费4250万元,如果按(1)中教育经费投入的增长率,到2019年该地区投入的教育经费是否能达到4250万元?请说明理由.
(参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近期末考试,心理专家建议考生可通过以下四种方式进行考前减压:![]() .享受美食,
.享受美食,![]() .交流谈心,
.交流谈心,![]() .体育锻炼,
.体育锻炼,![]() .欣赏艺术.
.欣赏艺术.
(1)随机采访一名九年级考生,选择其中某一种方式,他选择“享受美食”的概率是 .
(2)同时采访两名九年级考生,请用画树状图或列表的方法求他们中至少有一人选择“欣赏艺术”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为![]() ,看这栋大楼底部C的俯角为
,看这栋大楼底部C的俯角为![]() ,热气球A的高度为270米,则这栋大楼的高度为______米
,热气球A的高度为270米,则这栋大楼的高度为______米![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 交x轴于点A、点
交x轴于点A、点![]() 点A在点B的左边
点A在点B的左边![]() ,交y轴于点C,直线
,交y轴于点C,直线![]() 经过点B,交y轴于点D,且
经过点B,交y轴于点D,且![]() ,
,![]() .
.
![]() 求b、c的值;
求b、c的值;
![]() 点
点![]() 在第一象限,连接OP、BP,若
在第一象限,连接OP、BP,若![]() ,求点P的坐标,并直接判断点P是否在该抛物线上;
,求点P的坐标,并直接判断点P是否在该抛物线上;
![]() 在
在![]() 的条件下,连接PD,过点P作
的条件下,连接PD,过点P作![]() ,交抛物线于点F,点E为线段PF上一点,连接DE和BE,BE交PD于点G,过点E作
,交抛物线于点F,点E为线段PF上一点,连接DE和BE,BE交PD于点G,过点E作![]() ,垂足为H,若
,垂足为H,若![]() ,求
,求![]() 的值.
的值.
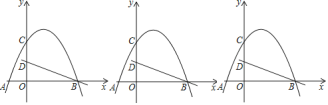
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
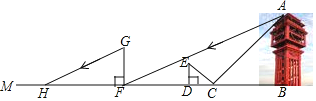
【题目】某市著名景点“凤凰楼”,一耸入云的文化丰碑,坐落于凤凰山之巅![]() 周末,阳光明媚,小明、小芳等同学一起登凤凰山,在山顶,他们想用一些测量工具和所学知识测量“凤凰楼”的高度来检验自己掌握知识和运用知识的能力
周末,阳光明媚,小明、小芳等同学一起登凤凰山,在山顶,他们想用一些测量工具和所学知识测量“凤凰楼”的高度来检验自己掌握知识和运用知识的能力![]() 他们经过观察发现,观测点与“凤凰楼”底部间的距离不易测得,因此他们运用如下方法来进行测量:如图,小芳在小明和“凤凰楼”之间的直线BM上放一平面镜,在镜面上做一个标记,这个标记在直线BM上对应位置为点C,镜子不动,小明看着镜面上的标记,他来回走动,走到点D时,看到“凤凰楼”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小明眼睛与地面的高度
他们经过观察发现,观测点与“凤凰楼”底部间的距离不易测得,因此他们运用如下方法来进行测量:如图,小芳在小明和“凤凰楼”之间的直线BM上放一平面镜,在镜面上做一个标记,这个标记在直线BM上对应位置为点C,镜子不动,小明看着镜面上的标记,他来回走动,走到点D时,看到“凤凰楼”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小明眼睛与地面的高度![]() 米,
米,![]() 米,然后,小明从点D沿DM方向走了24米,到达“凤凰楼”影子的末端F处,此时,测的小明身高FG的影长
米,然后,小明从点D沿DM方向走了24米,到达“凤凰楼”影子的末端F处,此时,测的小明身高FG的影长![]() 米,
米,![]() 米
米![]() 如图,已知
如图,已知![]() ,
,![]() ,
,![]() ,其中,测量时所使用的平面镜厚度忽略不计
,其中,测量时所使用的平面镜厚度忽略不计![]() 请你根据题中提供的相关信息,求出“凤凰楼”的高AB的长度.
请你根据题中提供的相关信息,求出“凤凰楼”的高AB的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com