
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 交x轴于点A、点
交x轴于点A、点![]() 点A在点B的左边
点A在点B的左边![]() ,交y轴于点C,直线
,交y轴于点C,直线![]() 经过点B,交y轴于点D,且
经过点B,交y轴于点D,且![]() ,
,![]() .
.
![]() 求b、c的值;
求b、c的值;
![]() 点
点![]() 在第一象限,连接OP、BP,若
在第一象限,连接OP、BP,若![]() ,求点P的坐标,并直接判断点P是否在该抛物线上;
,求点P的坐标,并直接判断点P是否在该抛物线上;
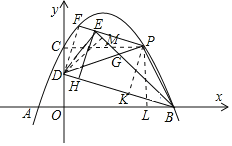
![]() 在
在![]() 的条件下,连接PD,过点P作
的条件下,连接PD,过点P作![]() ,交抛物线于点F,点E为线段PF上一点,连接DE和BE,BE交PD于点G,过点E作
,交抛物线于点F,点E为线段PF上一点,连接DE和BE,BE交PD于点G,过点E作![]() ,垂足为H,若
,垂足为H,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ,点P在抛物线上;(3)2.
,点P在抛物线上;(3)2.
【解析】
(1)直线y=kx-6k,令y=0,则B(6,0),便可求出点D、C的坐标,将B、C代入抛物线中,即可求得b、c的值;
(2)过点P,作![]() 轴于点L,过点B作
轴于点L,过点B作![]() 于点T,先求出点P的坐标为(4,4),再代入抛物线进行判断即可;
于点T,先求出点P的坐标为(4,4),再代入抛物线进行判断即可;
(3)连接PC,过点D作DM⊥BE于点M,先证△PCD≌△PLB,再分别证四边形EHKP、FDKP为矩形,求得![]() =2.
=2.
解:![]() 如图,直线
如图,直线![]() 经过点B,
经过点B,
令![]() ,则
,则![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,点
,点![]() ,
,
![]() 点B、C在抛物线
点B、C在抛物线![]() 上,
上,
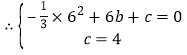 ,解得:
,解得:![]() ,
,
函数表达式为:![]() ;
;
![]() 如图,过点P,作
如图,过点P,作![]() 轴于点L,过点B作
轴于点L,过点B作![]() 于点T,
于点T,
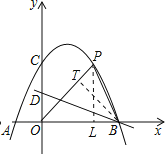
![]() ,
,
![]() ,
,![]() ,
,
![]() 点
点![]() 在第一象限,
在第一象限,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
故点P在抛物线上;
![]() 如图,连接PC,
如图,连接PC,
![]() ,
,![]() ,
,
![]() 轴,
轴,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
过点P作![]() 于点K,连接DF,
于点K,连接DF,
![]() ,
,![]() ,
,
![]() ,
,![]() 四边形EHKP为平行四边形,
四边形EHKP为平行四边形,
![]() ,
,![]() 四边形EHKP为矩形,
四边形EHKP为矩形,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
过点D作![]() 于点M,
于点M,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() 直线PF与BD解析式中的k值相等,
直线PF与BD解析式中的k值相等,
![]() ,
,
联立![]() 并解得:
并解得:![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 四边形FDKP为平行四边形,
四边形FDKP为平行四边形,
![]() ,
,![]() 四边形FDKP为矩形,
四边形FDKP为矩形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】某中学为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号):
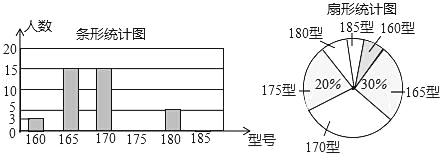
根据以上信息,解答下列问题:
(1)该班共有 名学生;
(2)补全条形统计图;
(3)该班学生所穿校服型号的众数为 ,中位数为 ;
(4)如果该校预计招收新生1500名,根据样本数据,估计新生穿170型校服的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点(A在B的左侧),且OA=3,OB=1,与y轴交于C(0,3),抛物线的顶点坐标为D(﹣1,4).
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)过点D作直线DE∥y轴,交x轴于点E,点P是抛物线上B、D两点间的一个动点(点P不与B、D两点重合),PA、PB与直线DE分别交于点F、G,当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.
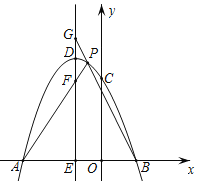
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 运动,速度为
运动,速度为![]() 个单位/
个单位/![]() ,在点
,在点![]() 运动的过程中,以
运动的过程中,以![]() 为圆心的圆始终与斜边
为圆心的圆始终与斜边![]() 相切,设⊙
相切,设⊙![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() (
(![]() )(
)(![]() ).
).
(1)当![]() 时,
时,![]() ;(用含
;(用含![]() 的式子表示)
的式子表示)
(2)求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)在⊙P运动过程中,当⊙P与三角形ABC的另一边也相切时,直接写出t的值.
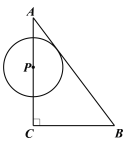
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,![]() ,点E在边CD上,且
,点E在边CD上,且![]() ,
,![]() 与
与![]() 关于AE所在的直线成对称图形
关于AE所在的直线成对称图形![]() 以点A为中心,把
以点A为中心,把![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,连接GF,则线段GF的长为______.
,连接GF,则线段GF的长为______.
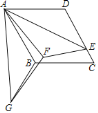
查看答案和解析>>
科目:初中数学 来源: 题型:
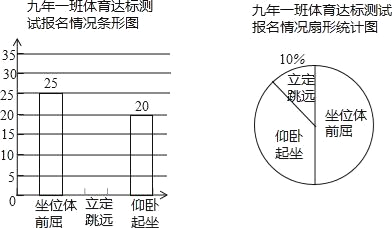
【题目】南岗区某中学的王老师统计了本校九年一班学生参加体育达标测试的报名情况,并把统计的数据绘制成了不完整的条形统计图和扇形统计图.根据图中提供的数据回答下列问题:
(1)该学校九年一班参加体育达标测试的学生有多少人?
(2)补全条形统计图的空缺部分;
(3)若该年级有1200名学生,估计该年级参加仰卧起坐达标测试的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
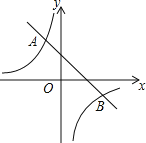
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象分别交于第二、四象限的A,B两点,点A的横坐标为
的图象分别交于第二、四象限的A,B两点,点A的横坐标为![]() .
.
![]() 求反比例函数的表达式;
求反比例函数的表达式;
![]() 根据图象回答:当x取何值时,
根据图象回答:当x取何值时,![]() 请直接写出答案:______.
请直接写出答案:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为12cm,点B,D之间的距离为16m,则线段AB的长为![]()
![]()
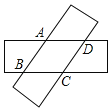
A. ![]() B. 10cmC. 20cmD. 12cm
B. 10cmC. 20cmD. 12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
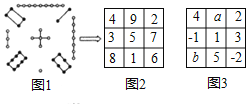
【题目】(阅读材料)“九宫图”源于我国古代夏禹时期的“洛书”![]() 图1所示
图1所示![]() ,是世界上最早的矩阵,又称“幻方”,用今天的数学符号翻译出来,“洛书”就是一个三阶“幻方”
,是世界上最早的矩阵,又称“幻方”,用今天的数学符号翻译出来,“洛书”就是一个三阶“幻方”![]() 图2所示
图2所示![]() .
.
(规律总结)观察图1、图2,根据“九宫图”中各数字之间的关系,我们可以总结出“幻方”需要满足的条件是______;若图3,是一个“幻方”,则![]() ______.
______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com