
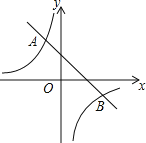
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象分别交于第二、四象限的A,B两点,点A的横坐标为
的图象分别交于第二、四象限的A,B两点,点A的横坐标为![]() .
.
![]() 求反比例函数的表达式;
求反比例函数的表达式;
![]() 根据图象回答:当x取何值时,
根据图象回答:当x取何值时,![]() 请直接写出答案:______.
请直接写出答案:______.
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
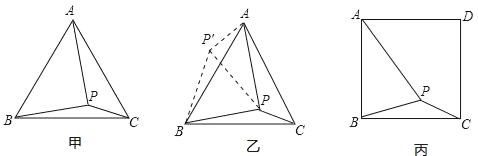
【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
解题思路是:将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′.
(1)△P′PB是 三角形,△PP′A是 三角形,∠BPC= °;
(2)利用△BPC可以求出△ABC的边长为 .
如图丙,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1;
,PC=1;
(3)求∠BPC度数的大小;
(4)求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近期末考试,心理专家建议考生可通过以下四种方式进行考前减压:![]() .享受美食,
.享受美食,![]() .交流谈心,
.交流谈心,![]() .体育锻炼,
.体育锻炼,![]() .欣赏艺术.
.欣赏艺术.
(1)随机采访一名九年级考生,选择其中某一种方式,他选择“享受美食”的概率是 .
(2)同时采访两名九年级考生,请用画树状图或列表的方法求他们中至少有一人选择“欣赏艺术”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 交x轴于点A、点
交x轴于点A、点![]() 点A在点B的左边
点A在点B的左边![]() ,交y轴于点C,直线
,交y轴于点C,直线![]() 经过点B,交y轴于点D,且
经过点B,交y轴于点D,且![]() ,
,![]() .
.
![]() 求b、c的值;
求b、c的值;
![]() 点
点![]() 在第一象限,连接OP、BP,若
在第一象限,连接OP、BP,若![]() ,求点P的坐标,并直接判断点P是否在该抛物线上;
,求点P的坐标,并直接判断点P是否在该抛物线上;
![]() 在
在![]() 的条件下,连接PD,过点P作
的条件下,连接PD,过点P作![]() ,交抛物线于点F,点E为线段PF上一点,连接DE和BE,BE交PD于点G,过点E作
,交抛物线于点F,点E为线段PF上一点,连接DE和BE,BE交PD于点G,过点E作![]() ,垂足为H,若
,垂足为H,若![]() ,求
,求![]() 的值.
的值.
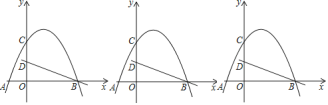
查看答案和解析>>
科目:初中数学 来源: 题型:
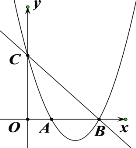
【题目】如图,在平面直角坐标系中,抛物线![]() 交x轴正半轴于点A、点B,交y轴于点C, 直线y=-x+6经过点B、点C;
交x轴正半轴于点A、点B,交y轴于点C, 直线y=-x+6经过点B、点C;
(1)求抛物线的解析式 ;
(2)点D在x轴下方的抛物线上,连接DB、DC,点D的横坐标为t,△BCD的面积为S,求S与t的函数关系式,并直接写出自变量t的取值范围 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
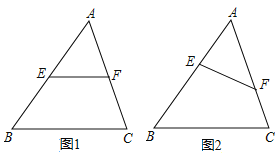
【题目】在△ABC 中,E、F 分别为线段 AB、AC 上的点(不与 A、B、C 重合)
(1)如图 1,若 EF//BC,求证:![]()
(2)如图 2,若 EF 不与 BC 平行,(1)中的结论是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
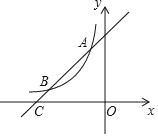
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求a,k的值及点B的坐标;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,直接写出点P的坐标.
S△BOC,直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com