
【题目】如图,直径为13的⊙E,经过原点O,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长分别是方程x2+kx+60=0的两根.
(1)OA:OB=____;
(2)若点C在劣弧OA上,连结BC交OA于D,当△BOC∽△BDA时,点D的坐标为______.
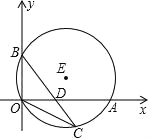
【答案】(1)12:5;(2)(![]() ,0).
,0).
【解析】
试题解析:连接AB,
∵∠AOB=90°,
∴AB是⊙E的直径,AB=13,
∴OA2+OB2=AB2=169.
根据根与系数的关系可得:
OA+OB=-k>0,OA×OB=60,
∴OA2+OB2=(OA+OB)2-2OAOB=k2-120=169,
∴k=-17,
原方程为x2-17x+60=0,
解得x1=5,x2=12,
∴OA=12,OB=5,
∴OA:OB=12:5.
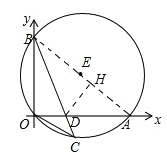
(2)过点D作DH⊥AB于H,如图.
∵△BOC∽△BDA,
∴∠OBC=∠DBA,
在△BOD和△BHD中,
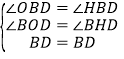 ,
,
∴△BOD≌△BHD,
∴BH=BO=5,DH=OD.
设OD=x,则DH=x,DA=12-x.
在Rt△DHA中,根据勾股定理可得,
x2+(13-5)2=(12-x)2,
解得x=![]() ,
,
∴点D的坐标为(![]() ,0).
,0).


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】(1)填空:如图,我们知道,一条线段OA绕着它的一个端点O旋转一周,另一个端点所形成的图形叫做 ;一个矩形ABCD绕着它的边AB旋转一周所形成的图形叫做 ;
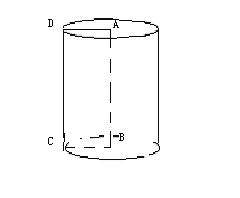
(2)如图,将一个直角三角形ABC(∠C=900)绕着它的直角边AC旋转一周,也能形成一个几何图形。
(a)在图中画出这个旋转图形的草图,并说出它的名称。
(b)如果ΔABC中AC=20,BC=15,把这个旋转图形沿着ΔABC的中位线DE且垂直于AC的方向横截,得到一个什么样的图形?并请你计算所截图形的上半部分的全面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
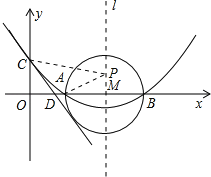
(1)求抛物线的解析式及A,B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)在以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
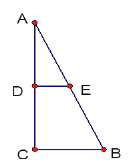
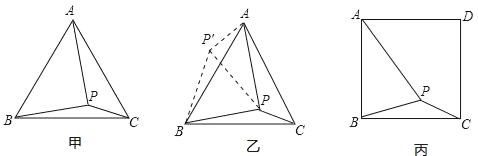
【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
解题思路是:将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′.
(1)△P′PB是 三角形,△PP′A是 三角形,∠BPC= °;
(2)利用△BPC可以求出△ABC的边长为 .
如图丙,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1;
,PC=1;
(3)求∠BPC度数的大小;
(4)求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形![]() 中,
中, ![]() ,垂足为
,垂足为![]() 与
与![]() 的延长线相交于
的延长线相交于![]() ,且
,且![]() ,连接
,连接![]() ;
;
(1)如图![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
(2)如图![]() ,连接
,连接![]() ,若
,若![]() ,在不添加任何辅助线的情况下,直接写出图
,在不添加任何辅助线的情况下,直接写出图![]() 中所有面积等于
中所有面积等于![]() 的面积的钝角三角形.
的面积的钝角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
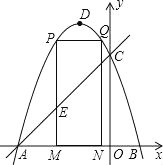
【题目】如图,抛物线y=﹣x2﹣2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM.如图,点P在点Q左边,试用含m的式子表示矩形PQNM的周长;
(3)当矩形PQNM的周长最大时,m的值是多少?并求出此时的△AEM的面积;
(4)在(3)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=2![]() DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近期末考试,心理专家建议考生可通过以下四种方式进行考前减压:![]() .享受美食,
.享受美食,![]() .交流谈心,
.交流谈心,![]() .体育锻炼,
.体育锻炼,![]() .欣赏艺术.
.欣赏艺术.
(1)随机采访一名九年级考生,选择其中某一种方式,他选择“享受美食”的概率是 .
(2)同时采访两名九年级考生,请用画树状图或列表的方法求他们中至少有一人选择“欣赏艺术”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
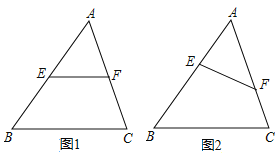
【题目】在△ABC 中,E、F 分别为线段 AB、AC 上的点(不与 A、B、C 重合)
(1)如图 1,若 EF//BC,求证:![]()
(2)如图 2,若 EF 不与 BC 平行,(1)中的结论是否仍然成立?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com