
【题目】如图,在△ABC中,AB=AC,∠BAC=90°.
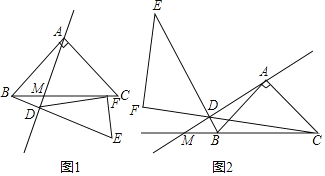
(1)如图1,若直线AD与BC相交于M,过点B作AM的垂线,垂足为D,连接CD并延长BD至E,使得DE=DC,过点E作EF⊥CD于F,证明:AD=EF+BD.
(2)如图2,若直线AD与CB的延长线相交于M,过点B作AM的垂线,垂足为D,连接CD并延长BD至E,使得DE=DC,过点E作EF⊥CD交CD的延长线于F,探究:AD、EF、BD之间的数量关系,并证明.
【答案】(1)见解析;(2)AD+BD=EF,理由见解析.
【解析】
(1)将△ABD绕点A逆时针方向旋转90°至△ACG,得到BD=CG,延长GC交DE于点H,证明四边形ADHG为正方形,则AD=GH,证明△DEF≌△DCH,得到EF=CH,则得出结论;
(2)作CN⊥AM,证明△DEF≌△CDN,得到EF=DN,证明△ADB≌△CNA.得到BD=AN.则AD+AN=DN=EF.
证明:(1)∵AB=AC,∠BAC=90°,
∴△ABC为等腰直角三角形,
如图1,将△ABD绕点A逆时针方向旋转90°至△ACG,
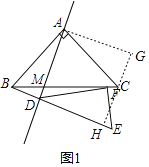
∴BD=CG,
延长GC交DE于点H,
∵AD⊥BE,∠DAG=∠AGC=90°,AD=AG,
∴四边形ADHG为正方形,
∴∠DHC=90°,
∴AD=GH,
∵DE=DC,EF⊥CD,∠EDF=∠CDH,
∴△DEF≌△DCH(AAS),
∴EF=CH,
∴AD=GH=GC+CH=EF+BD;
(2)AD+BD=EF,理由如下:
作CN⊥AM,

∵AD⊥BE,
∴∠EDF+∠ADC=90°,
∵∠DCN+∠ADC=90°,
∴∠EDF=∠DCN,
∵∠F=∠DNC=90°,DE=DC,
∴△DEF≌△CDN(AAS),
∴EF=DN,
∵∠BAC=90°,
∴∠DAB+∠NAC=90°,
又∵∠DAB+∠DBA=90°,
∴∠NAC=∠DBA,
∵AB=AC,
∴△ADB≌△CNA(AAS).
∴BD=AN.
∴AD+AN=DN=EF,
∴AD+BD=EF.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线与![]() 轴交于点A,与
轴交于点A,与![]() 轴交点C,抛物线
轴交点C,抛物线![]() 过A,C两点,与x轴交于另一点B.
过A,C两点,与x轴交于另一点B.
(1)求抛物线的解析式.
(2)在直线AC上方的抛物线上有一动点E,连接BE,与直线AC相交于点F,当![]() 时,求sin∠EBA的值.
时,求sin∠EBA的值.
(3)点N是抛物线对称轴上一点,在(2)的条件下,若点E位于对称轴左侧,在抛物线上是否存在一点M,使以M,N,E,B为顶点的四边形是平行四边形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
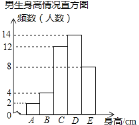
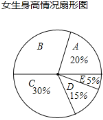
【题目】某校为了了解学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成下面的统计图表:
组别 | A | B | C | D | E |
身高(cm) | x<150 | 150≤x<155 | 155≤x<160 | 160≤x<165 | x≥165 |
根据图表中信息,回答下列问题:
(1)在样本中,男生身高的中位数落在 组(填组别序号),女生身高在B组的人数有 人;
(2)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生约有多少人?
(3)从男生样本的A、B两组里,随机安排2人参加一项活动,求恰好是1人在A组、1人在B组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生物学上研究表明:不同浓度的生长素对植物的生长速度影响不同,在一定范围内,生长素的浓度对植物的生长速度有促进作用,相反,在某些浓度范围,生长速度会变缓慢,甚至阻碍植物生长(阻碍即植物不生长,甚至枯萎).小林同学在了解到这一信息后,决定研究生长素浓度与茶树生长速度的关系,设生长素浓度为x克/升,生长速度为y毫米/天,当x超过4时,茶树的生长速度y与生长素x浓度满足关系式:![]() .实验数据如下表,当生长速度为0时,实验结束.
.实验数据如下表,当生长速度为0时,实验结束.
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 2 | 4 | 6 | 8 | 10 | 9 | 7 | 4 | 0 |
(1)如图,建立平面直角坐标系xOy,描出表中各对对应值为坐标的点,画出该函数图象;
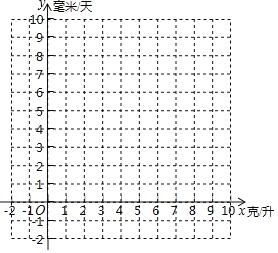
(2)根据上述表格,求出整个实验过程中y与x的函数关系式,并写出自变量x的取值范围;
(3)结合画出的函数图象,写出该函数的一条性质: ;
(4)若直线y=kx+3与上述函数图象有2个交点,则k的取值范围是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,y是关于
,y是关于![]() 的二次函数,抛物线
的二次函数,抛物线![]() 经过点
经过点![]() .抛物线
.抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 则下列判断:
则下列判断:
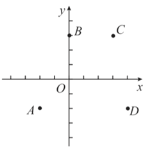
①四条抛物线的开口方向均向下;
②当![]() 时,四条抛物线表达式中的
时,四条抛物线表达式中的![]() 均随
均随![]() 的增大而增大;
的增大而增大;
③抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 顶点的上方;
顶点的上方;
④抛物线![]() 与
与![]() 轴交点在点
轴交点在点![]() 的上方.
的上方.
其中正确的是
A.①②④B.①③④
C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生新冠疫情防控期间每天居家体育活动的时间(单位:![]() ),在网上随机调查了该校九年级部分学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
),在网上随机调查了该校九年级部分学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
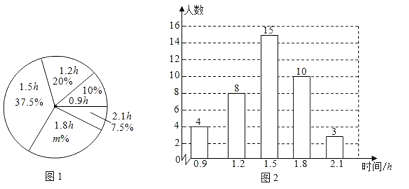
(1)本次接受调查的初中学生人数为________,图①中![]() 的值为________;
的值为________;
(2)这组数据的平均数是________,众数是________,中位数是________;
(3)根据统计的这组每天居家体育活动时间的样本数据,估计该校500名九年级学生居家期间每天体育活动时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
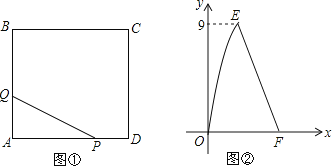
【题目】如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
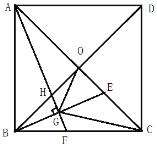
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(不与O、C重合),作AF⊥BE,垂足为G,分别交BC、OB于F、H,连接OG、CG.
(1)求证:AH=BE;
(2)∠AGO的度数是否为定值?说明理由;
(3)若∠OGC=90°,BG=![]() ,求△OGC的面积.
,求△OGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 直径,以
直径,以![]() 为边作等腰
为边作等腰![]() ,且
,且![]() ,
,![]() 与边
与边![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,并交
,并交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)若![]() ,
,![]() °,求由线段
°,求由线段![]() 、
、![]() 及
及![]() 所围成的图形(阴影部分)面积.
所围成的图形(阴影部分)面积.
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com