
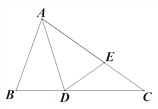
【题目】如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,E为AC上一点,AE=AB,连接DE.
(1)求证:△ABD≌△AED;
(2)已知BD=5,AB=9,求AC长.
【答案】(1)证明见解析; (2)AC=14
【解析】
试题(1)由AD是∠BAC的平分线,得出∠BAD=∠DAC,根据已知条件可证△ABD≌△AED;
(2)由△ABD≌△AED 得BD=DE,∠B=∠AED,再利用三角形外角的性质求证CE=DE,然后问题可解.
试题解析:(1)∵∠BAC的平分线AD交BC边于点D,
∴∠BAD=∠DAC,
在△ABD与△AED中,
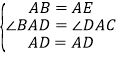 ,
,
∴△ABD≌△AED(SAS);
(2)∵△ABD≌△AED
∴BD=DE,∠B=∠AED,
∵∠B=2∠C,∠AED=∠C+∠EDC,
∴∠AED=2∠C,
∴∠C=∠EDC,
∴CE=DE,
∴CE=BD,
∴AC=AE+EC=AB+BD.
∵BD=5,AB=9
∴AC=14.


科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”. 应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )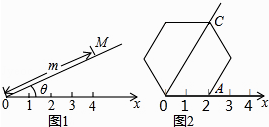
A.(60°,4)
B.(45°,4)
C.(60°,2 ![]() )
)
D.(50°,2 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方
向依次不断移动,每次移动1个单位,其行走路线如下图所示.

(1)填写下列各点的坐标:A4( , )、A8( , )、A12( , );
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A100到点A101的移动方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用大小相等的小正方形按一定规律拼成的,则第10个图形是_________个小正方形,第n 个图形是___________个小正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,我市组织了一次初三年级1 200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
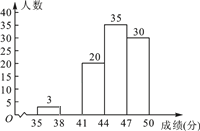
成绩分组 | 频数 | 频率(百分比) |
35≤x<38 | 3 | 0.03 |
38≤x<41 | a | 0.12 |
41≤x<44 | 20 | 0.20 |
44≤x<47 | 35 | 0.35 |
47≤x≤50 | 30 | b |
请根据所提供的信息解答下列问题:
(1)频率统计表中a=________,b=_______;
(2)请补全频数分布直方图;
(3)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程x2+(2k+1)x+k2+2=0有两个实数根x1、x2
(1)求实数k的取值范围;
(2)若x1、x2满足|x1|+|x2|=|x1x2|﹣1,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com