
【题目】关于x的方程x2+(2k+1)x+k2+2=0有两个实数根x1、x2
(1)求实数k的取值范围;
(2)若x1、x2满足|x1|+|x2|=|x1x2|﹣1,求k的值.
【答案】
(1)解:根据题意得△=(2k+1)2﹣4(k2+2)≥0,
解得k≥ ![]()
(2)解:根据题意得x1+x2=﹣(2k+1)<0,x1x2=k2+2>0,
∴x1<0,x2<0,
∵|x1|+|x2|=|x1x2|﹣1,
∴﹣(x1+x2)=x1x2﹣1,
∴2k+1=k2+2﹣1,
整理得k2﹣2k=0,解得k1=0,k2=2,
∵k≥ ![]() ,
,
∴k=2
【解析】(1)根据判别式的意义得到△=(2k+1)2﹣4(k2+2)≥0,然后解不等式即可;(2)根据根与系数的关系得到x1+x2=﹣(2k+1)<0,x1x2=k2+2>0,则利用有理数的乘法性质可判断x1<0,x2<0,然后去绝对值得到﹣(x1+x2)=x1x2﹣1,则2k+1=k2+2﹣1,整理得到k2﹣2k=0,再解关于k的方程即可得到满足条件的k的值.


科目:初中数学 来源: 题型:
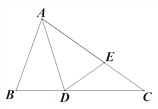
【题目】如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,E为AC上一点,AE=AB,连接DE.
(1)求证:△ABD≌△AED;
(2)已知BD=5,AB=9,求AC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,﹣2),顶点为D,点E的坐标为(0,﹣1),该抛物线于BE交于另一点F,连接BC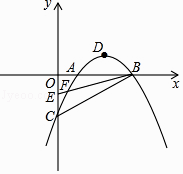
(1)求该抛物线的解析式;
(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;
(3)一动点M从点D出发,以每秒1个单位的速度沿平行于y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),点M在运动过程中,当t为何值时,∠OMB=90°?
(4)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,直接写出点P的坐标;若不存在,请说明利由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在数轴上,从点A出发,沿数轴向右移动3个单位长度到达点C,点B所表示的有理数是5的相反数,按要求完成下列各小题.
(1)请在数轴上标出点B和点C;
(2)求点B所表示的有理数与点C所表示的有理数的乘积;
(3)若将该数轴进行折叠,使得点A和点B重合,则点C和数 所表示的点重合.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(-3,0),B(1,0).
(1)在y轴上找一点C,使之满足S△ABC=6,求点C的坐标;
(2)在y轴上找一点D,使AD=AB,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家批发商出售同样品牌的茶壶和茶杯,定价相同,茶壶每把30元,茶杯每只5元.两家都在进行优惠销售:甲店买一送一大酬宾(买一把茶壶赠送茶杯一只);乙店全场9折优惠(按实际价格的90%收费).某茶具店需茶壶5把,茶杯若干只(不少于5只).
(1)若设购买茶杯x只(x>5),则在甲店购买需付_____元,在乙店购买需付_____元;(用含x的代数式表示)
(2)当茶具店需购买10只茶杯时,到哪家商店购买较便宜?试加以说明;
(3)试求出当茶具店购买多少只茶杯时,在两家商店购买所需付的款一样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距400km,甲、乙两车分别从A、B两地同时出发,相向而行,甲车以每小时100km的速度匀速行驶1h后,休息了1h,然后按原速继续行驶到B地,乙车以每小时80km的速度匀速行驶到A地.
(1)当乙车经过甲车休息的地方时,乙车行驶的时间是 h;
(2)当甲、乙两车相遇时,求乙车行驶的时间;
(3)当甲、乙两车相距40km时,求乙车行驶的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,M、E、F三点在 ![]() 上,N是矩形两对角线的交点.若
上,N是矩形两对角线的交点.若 ![]() =24,
=24, ![]() =32,
=32, ![]() =16,
=16, ![]() =8,
=8, ![]() =7,则下列哪一条直线是A、C两点的对称轴?( )
=7,则下列哪一条直线是A、C两点的对称轴?( ) 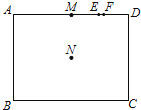
A.直线MN
B.直线EN
C.直线FN
D.直线DN
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com