练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，6个形状、大小完全相同的菱形组成网格，已知菱形的一个角∠O为60°，A，B，C都在格点上，则tan∠ABC的值为 ．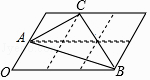

    【答案】
    【解析】解：设菱形的边长为a，由题意得∠AEF=30°，∠BEF=60°，AE= a，EB=2a， ∴∠AEC=90°，
    在Rt△AEB中，tan∠ABC= = ．
    所以答案是： ．

    【考点精析】本题主要考查了菱形的性质和解直角三角形的相关知识点，需要掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知关于x的方程2（x+1）﹣m=﹣的解比方程5（x﹣1）﹣1=4（x﹣1）+1的解大2．

    （1）求第二个方程的解；

    （2）求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请根据图中提供的信息,回答下列问题

    （1）一个暖瓶与一个水杯分别是多少元?

    （2）甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定： 这两种商品都打九折；乙商场规定：买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯，请问选择哪家商场购买更合算，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

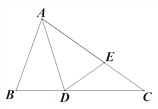
    【题目】如图，在△ABC中，∠ABC=2∠C，∠BAC的平分线AD交BC于D，E为AC上一点，AE＝AB,连接DE.

    （1）求证：△ABD≌△AED；

    （2）已知BD=5，AB=9，求AC长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，P是BC边上不同于B，C的一动点，过点P作PQ⊥AB，垂足为Q，连接AP．若AC=3，BC=4，则△AQP的面积的最大值是（ ）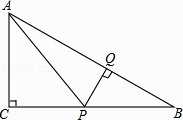
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了对学生进行爱国主义教育，某校组织学生去看演出，有甲乙两种票，已知甲乙两种票的单价比为4：3，单价和为42元.

    （1）甲乙两种票的单价分别是多少元？

    （2）学校计划拿出不超过750元的资金，让七年级一班的36名学生首先观看，且规定购买甲种票必须多于15张，有哪几种购买方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，D，E是BC边上的两点，AD＝AE，BE＝CD，∠1＝∠2＝110°，∠BAE＝60°，则∠CAD的度数为(　　)

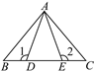
    A. 50° B. 60° C. 70° D. 110°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=ax2+bx+c与x轴交于A（1，0），B（3，0），与y轴交于C（0，﹣2），顶点为D，点E的坐标为（0，﹣1），该抛物线于BE交于另一点F，连接BC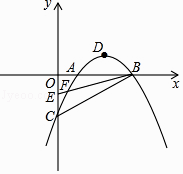

    （1）求该抛物线的解析式；
    （2）若点H（1，y）在BC上，连接FH，求△FHB的面积；
    （3）一动点M从点D出发，以每秒1个单位的速度沿平行于y轴方向向上运动，连接OM，BM，设运动时间为t秒（t＞0），点M在运动过程中，当t为何值时，∠OMB=90°？
    （4）在x轴上方的抛物线上，是否存在点P，使得∠PBF被BA平分？若存在，直接写出点P的坐标；若不存在，请说明利由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A、B两地相距400km，甲、乙两车分别从A、B两地同时出发，相向而行，甲车以每小时100km的速度匀速行驶1h后，休息了1h，然后按原速继续行驶到B地，乙车以每小时80km的速度匀速行驶到A地．

    （1）当乙车经过甲车休息的地方时，乙车行驶的时间是　 　h；

    （2）当甲、乙两车相遇时，求乙车行驶的时间；

    （3）当甲、乙两车相距40km时，求乙车行驶的时间．

    查看答案和解析>>

    同步练习册答案