
 二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,点A1,A2,A3…A2010在y轴的正半轴上,点B1,B2,B3,…B2010,在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…△A2009B2010A2010都为等边三角形,则△A2009B2010A2010的周长=6030.
二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,点A1,A2,A3…A2010在y轴的正半轴上,点B1,B2,B3,…B2010,在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…△A2009B2010A2010都为等边三角形,则△A2009B2010A2010的周长=6030. 分析 作B1C⊥y轴于C,B2D⊥y轴于D,B3E⊥y轴于E,如图,设AOC=t,根据等边三角形的性质得B1C=$\sqrt{3}$AOC,则B1($\sqrt{3}$t,t),利用二次函数图象上点的坐标特征得到t=$\frac{2}{3}$•($\sqrt{3}$t)2,解得t1=0(舍去),t2=$\frac{1}{2}$,于是得到OA1=1,即△A0B1A1边长为1,即A1(0,1);再设A1D=m,同样设B2($\sqrt{3}$m,m+1),则m+1=$\frac{2}{3}$•($\sqrt{3}$m)2,解得m1=-$\frac{1}{2}$(舍去),M2=1,又可得到A1A2=2A1D=2,即△A1B2A2边长为2,同理可得△A2B3A3的边长为3,根据此规律可判断△A2009B2010A2010的边长为2010,然后计算△A2009B2010A2010的周长.
解答 解:作B1C⊥y轴于C,B2D⊥y轴于D,B3E⊥y轴于E,如图,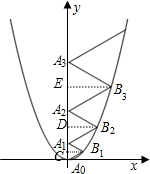 设AOC=t,
设AOC=t,
∵△A0B1A1为等边三角形,
∴B1($\sqrt{3}$t,t),
∴t=$\frac{2}{3}$•($\sqrt{3}$t)2,解得t1=0(舍去),t2=$\frac{1}{2}$,
∴B1($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),
∴OA1=1,即△A0B1A1边长为1;
∴A1(0,1),
设A1D=m,
∵△A1B2A2为等边三角形,
∴B2($\sqrt{3}$m,m+1),
∴m+1=$\frac{2}{3}$•($\sqrt{3}$m)2,解得m1=-$\frac{1}{2}$(舍去),M2=1,
∴A1A2=2A1D=2,即△A1B2A2边长为2,
同理可得△A2B3A3的边长为3,
∴△A2009B2010A2010的边长为2010,
∴△A2009B2010A2010的周长=3×2010=6030.
故答案为6030.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了等边三角形的性质.


科目:初中数学 来源: 题型:解答题
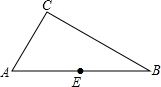 如图,△ABC中,∠CAB=60°,∠B=30°,E是AB的中点.
如图,△ABC中,∠CAB=60°,∠B=30°,E是AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 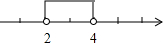 | B. | 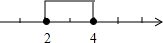 | ||
| C. | 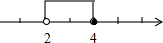 | D. | 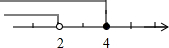 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
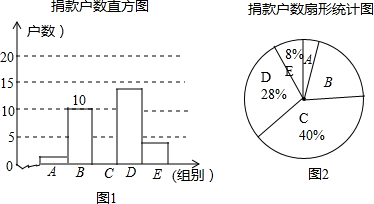 我市政府积极组织社区居民为希望工程捐款,为了解阳光社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图.已知A、B两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题
我市政府积极组织社区居民为希望工程捐款,为了解阳光社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图.已知A、B两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题| 组别 | 捐款额(x)元 |
| A | 10≤x<100 |
| B | 100≤x<200 |
| C | 200≤x<300 |
| D | 300≤x<400 |
| E | x≥400 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com