
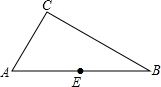
 如图,△ABC中,∠CAB=60°,∠B=30°,E是AB的中点.
如图,△ABC中,∠CAB=60°,∠B=30°,E是AB的中点.分析 (1)直接利用角平分线的作法得出答案;
(2)①根据角平分线性质结合等腰三角形的性质求出CD=DE,根据HL定理求出另三角形全等即可;
②求出∠DEB=90°,DE=1,根据含30度角的直角三角形性质求出即可.
解答 解:(1)如图所示:AD即为所求;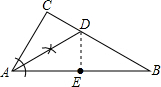 (2)①证明:∵AD平分∠CAB,∠CAB=60°,∠B=30°,
(2)①证明:∵AD平分∠CAB,∠CAB=60°,∠B=30°,
∴∠CAD=∠DAE=∠B=30°,
∴CD=DE,
∵E是AB的中点,
∴DE⊥AB,
∵在Rt△ACD和Rt△AED中
$\left\{\begin{array}{l}{AD=AD}\\{CD=DE}\end{array}\right.$
∴Rt△ACD≌Rt△AED(HL);
②解:∵DC=DE=1,DE⊥AB,
∴∠DEB=90°,
∵∠B=30°,
∴BD=2DE=2.
点评 本题考查了全等三角形的判定、角平分线性质、含30度角的直角三角形性质的应用等知识,得出DE⊥AB是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
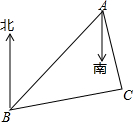 如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向.
如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,点A1,A2,A3…A2010在y轴的正半轴上,点B1,B2,B3,…B2010,在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…△A2009B2010A2010都为等边三角形,则△A2009B2010A2010的周长=6030.
二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,点A1,A2,A3…A2010在y轴的正半轴上,点B1,B2,B3,…B2010,在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…△A2009B2010A2010都为等边三角形,则△A2009B2010A2010的周长=6030.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 根据《吉林省2007年国民经济和社会发展统计公报》得知,全省人口构成如下表,单位:万人
根据《吉林省2007年国民经济和社会发展统计公报》得知,全省人口构成如下表,单位:万人| 指标 | 2007年 |
| 0-14岁 | 371.26 |
| 15-64岁 | |
| 65岁及以上 | 229.30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com