
 如图,在△ABC中,AB=AC,点D、E是边BC上的两个点,且BD=DE=EC,过点C作CF∥AB交AE延长线于点F,连接FD并延长与AB交于点G;
如图,在△ABC中,AB=AC,点D、E是边BC上的两个点,且BD=DE=EC,过点C作CF∥AB交AE延长线于点F,连接FD并延长与AB交于点G;分析 (1)由BD=DE=EC知BE=2CE,由CF∥AB证△ABE∽△FCE得$\frac{AB}{FC}=\frac{BE}{CE}$=2,即AB=2FC,根据AB=AC即可得证;
(2)由∠1=∠B证△DAG∽△BAD得∠AGD=∠ADB,即∠B+∠2=∠5+∠6,结合∠B=∠5、∠2=∠3得∠3=∠6,再由CF∥AB得∠4=∠B,继而知∠4=∠5,即可证△ACD∽△DCF得CD2=AC•CF.
解答 证明:(1)∵BD=DE=EC,
∴BE=2CE,
∵CF∥AB,
∴△ABE∽△FCE,
∴$\frac{AB}{FC}=\frac{BE}{CE}$=2,即AB=2FC,
又∵AB=AC,
∴AC=2CF;
(2)如图,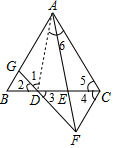
∵∠1=∠B,∠DAG=∠BAD,
∴△DAG∽△BAD,
∴∠AGD=∠ADB,
∴∠B+∠2=∠5+∠6,
又∵AB=AC,∠2=∠3,
∴∠B=∠5,
∴∠3=∠6,
∵CF∥AB,
∴∠4=∠B,
∴∠4=∠5,
则△ACD∽△DCF,
∴$\frac{CD}{CF}=\frac{AC}{DC}$,即CD2=AC•CF.
点评 本题主要考查相似三角形的判定与性质,熟练掌握三角形外角性质和平行线的性质得出三角形相似所需要的条件是解题的关键.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{12}{5}$ | B. | $\frac{5}{12}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{sinα}$ | B. | 2sinα | C. | $\frac{2}{cosα}$ | D. | 2cosα |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,4) | B. | (1,2) | C. | (3,2) | D. | (1,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小明家所在小区的前后两栋楼AB、CD,小明在自己所住楼AB的底部A处,利用对面楼CD墙上玻璃(与地面垂直)的反光,测得楼AB顶部B处的仰角是α,若tanα=0.45,两楼的间距为30米,则小明家所住楼AB的高度是27米.
如图,小明家所在小区的前后两栋楼AB、CD,小明在自己所住楼AB的底部A处,利用对面楼CD墙上玻璃(与地面垂直)的反光,测得楼AB顶部B处的仰角是α,若tanα=0.45,两楼的间距为30米,则小明家所住楼AB的高度是27米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com