
【题目】如图、在三角形 ABC 中,B(2,0),把三角形 ABC 沿AC 边平移,使 A 点到 C 点,△ABC 变换为△DCE.已知 C(0,3.5) 请写出 A、D、E 的坐标,并说出平移的过程。(书写时沿着 x 轴平 移,再沿着 y 轴平移。)
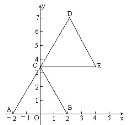
【答案】A(-2,0)D(2,7)E(4,3.5),把△ABC向右平移2个单位长度,再向上平移3.5个单位长度得到△CED.
【解析】
根据图象△ABC可得A(-2,0),再根据平移后△CED的图象可得D(2,7),E(4,3.5),再根据图象叙述平移过程即可.
(1)由题意得:A(-2,0),B(2,0),
∵C(0,3.5),点A移到点C,
∴△ABC平移到△CED,对应点的坐标的变化的规律为横坐标加2,纵坐标加3.5.
∴点C(0,3.5)对应的点D的坐标为(2,7),点B(2,0)对应的点E的坐标为(4,3.5);
(2)把△ABC向右平移2个单位长度,再向上平移3.5个单位长度得到△CED.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作对角线等于已知线段的菱形.
 已知:两条线段a、b.
已知:两条线段a、b.
求作:菱形AMBN,使得其对角线分别等于b和2a.
尺规作图:作对角线等于已知线段的菱形.
 已知:两条线段a、b.
已知:两条线段a、b.
求作:菱形AMBN,使得其对角线分别等于b和2a.
小军的作法如下:
如图
(1)画一条线段AB等于b;
(2)分别以A、B为圆心,大于![]() AB的长为半径,
AB的长为半径,
在线段AB的上下各作两条弧,两弧相交于P、Q两点;
(3)作直线PQ交AB于O点;
(4)以O点为圆心,线段a的长为半径作两条弧,交直线PQ于M、N两点,连接AM、AN、BM、BN.所以四边形AMBN就是所求的菱形.
如图
(1)画一条线段AB等于b;
(2)分别以A、B为圆心,大于![]() AB的长为半径,
AB的长为半径,
在线段AB的上下各作两条弧,两弧相交于P、Q两点;
(3)作直线PQ交AB于O点;
(4)以O点为圆心,线段a的长为半径作两条弧,交直线PQ于M、N两点,连接AM、AN、BM、BN.所以四边形AMBN就是所求的菱形.
老师说:“小军的作法正确.”
该上面尺规作图作出菱形AMBN的依据是_______________________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AC是对角线.将长方形ABCD绕点B顺时针旋转90°到长方形GBEF位置,H是EG的中点.若AB=6,BC=8,则线段CH的长为( )
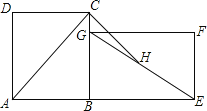
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠MON=90°,△ABC中,∠C=90°,AC=3cm,BC=4cm,将△ABC的两个顶点A、B放在射线OM和ON上移动,作CD⊥ON于点D,记OA=x(当点O与A重合时,x的值为0),CD=y.
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整.

(1)通过取点、画图、计算、测量等方法,得到了x与y的几组值,如下表(补全表格)
x/cm | 0 | 1 | 2 | 3 | 4 | 4.5 | 5 |
y/cm | 2.4 | 3.0 | 3.5 | 3.9 | 4.0 | 3.9 |
|
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题;当x的值为 时,线段OC长度取得最大值为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校小组利用暑假中前40天参加社会实践活动,参与了一家网上书店经营,了解到一种成本每本20元的书在x天销售量P=50﹣x.在第x天的售价每本y元,y与x的关系如图所示. 已知当社会实践活动时间超过一半后.y=20+ ![]()

(1)请求出当1≤x≤20时,y与x的函数关系式,并求出第12天此书的销售单价;
(2)这40天中该网点销售此书第几天获得的利润最大?最大的利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:![]() ,则
,则![]() 是“和谐分式”.
是“和谐分式”.
(1)下列分式中,属于“和谐分式”的是_____(填序号);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(2)将“和谐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() =_______(要写出变形过程);
=_______(要写出变形过程);
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,AF∥CE,且交BC于点F. 
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com