
分析 根据线段中点的性质,可得AM的长,根据N是AM的三等分点,可得AN的长,根据线段的和差,可得答案.
解答 解:①如图: ,
,
由M是AB的中点,得
AM=$\frac{1}{2}$AB=$\frac{1}{2}$×12=6cm,
由N是AM的三等分点,的
AN=$\frac{1}{3}$AM=$\frac{1}{3}$×6=2cm,
由线段的和差,得
BN=AB-AN=12-2=10cm;
②如图: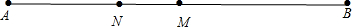 ,
,
由M是AB的中点,得
AM=$\frac{1}{2}$AB=$\frac{1}{2}$×12=6cm,
由N是AM的三等分点,的
AN=$\frac{2}{3}$AM=$\frac{2}{3}$×6=4cm,
由线段的和差,得
BN=AB-AN=12-4=8cm;
综上所述:线段BN的长是10cm或8cm.
故答案为:10cm或8cm.
点评 本题考查了两点间的距离,利用N是AM的三等分点得出AN的长是解题关键.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
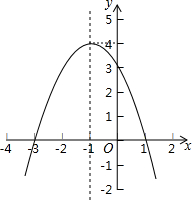 已知抛物线y=ax2+bx+c如图所示,请结合图象中所给信息完成以下问题:
已知抛物线y=ax2+bx+c如图所示,请结合图象中所给信息完成以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,射线OM上有三点A、B、C,满足OA=60cm,AB=60cm,BC=10cm(如图所示),点P从点O出发,沿OM方向以1cm/秒的速度匀速运动.
如图,射线OM上有三点A、B、C,满足OA=60cm,AB=60cm,BC=10cm(如图所示),点P从点O出发,沿OM方向以1cm/秒的速度匀速运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
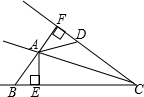 如图,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F.
如图,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,抛物线y=x2-2x-3交x轴于A(-1,0)、B(3,0),交y轴于C(0,-3),M是抛物线的顶点,现将抛物线沿平行于y轴的方向向上平移三个单位,则曲线CMB在平移过程中扫过的面积为9(面积单位).
如图,抛物线y=x2-2x-3交x轴于A(-1,0)、B(3,0),交y轴于C(0,-3),M是抛物线的顶点,现将抛物线沿平行于y轴的方向向上平移三个单位,则曲线CMB在平移过程中扫过的面积为9(面积单位).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com