
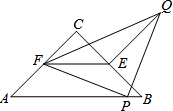
 如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )
如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
分析 取AB中点D,连接FD,根据等腰直角三角形的性质,由△ABC为等腰直角三角形得到AC=BC,∠A=45°,再根据点D、E、F分别是△ABC三边的中点,则AD=BD=4,DP=3,EF为△ABC的中位线,于是可判断△ADF为等腰直角三角形,得到∠FDA=45°,利用三角形中位线的性质得EF∥AB,EF=$\frac{1}{2}$AB=5,根据平行线性质得∠EFP+∠DFP=45°;又由于△PQF为等腰直角三角形,则∠EFP+∠EFQ=45°,所以∠DFP=∠EFQ,然后根据有两组对应边成比例且夹角相等的三角形相似,得出△FDP∽△FEQ,再根据相似三角形的对应边成比例即可求得.
解答 解:连结FD,D是AB的中点,如图,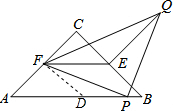 ∵△ABC为等腰直角三角形,AB=10,PB=1,
∵△ABC为等腰直角三角形,AB=10,PB=1,
∴AC=BC=5$\sqrt{2}$,∠A=45°,
∵点D、E、F分别是△ABC三边的中点,AB=10,PB=1,
∴AD=BD=5,DP=DB-PB=5-1=4,EF、DF为△ABC的中位线,
∴EF∥AB,EF=$\frac{1}{2}$AB=5,DF=$\frac{1}{2}$BC=$\frac{5}{2}$$\sqrt{2}$,∠EFP=∠FPD,
∴∠FDA=45°,$\frac{DF}{EF}$=$\frac{\frac{5\sqrt{2}}{2}}{5}$=$\frac{\sqrt{2}}{2}$,
∴∠DFP+∠DPF=45°,
∵△PQF为等腰直角三角形,
∴∠PFE+∠EFQ=45°,FP=PQ,
∴∠DFP=∠EFQ,
∵△PFQ是等腰直角三角形,
∴$\frac{PF}{EQ}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{DF}{EF}$=$\frac{PF}{FQ}$,
∴△FDP∽△FEQ,
∴$\frac{QE}{DP}$=$\frac{EF}{FD}$=$\sqrt{2}$,
∴QE=$\sqrt{2}$DP=4$\sqrt{2}$.
故选D.
点评 本题考查的是等腰直角三角形,相似三角形的判定等知识,根据题意作出辅助线,构造出三角形的中位线是解答此题的关键.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,PN+PM+MN的最小值是5cm,则∠AOB的度数是30°.
如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,PN+PM+MN的最小值是5cm,则∠AOB的度数是30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
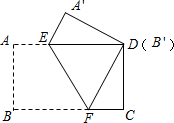 把一张长方形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,求:
把一张长方形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com