
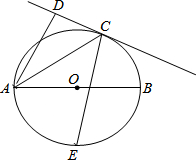
 如图,AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD,垂足为D,E是弧AB的中点,若AD=$\frac{32}{5}$,AC=8,则CE的长为( )
如图,AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD,垂足为D,E是弧AB的中点,若AD=$\frac{32}{5}$,AC=8,则CE的长为( )| A. | 7$\sqrt{2}$ | B. | 7$\sqrt{3}$ | C. | 8$\sqrt{2}$ | D. | 3+4$\sqrt{2}$ |
分析 首先连接OC,由直线CD与⊙O相切于点C,AD⊥CD,易证得OC∥AD,继而可得AC平分∠DAB,然后连接BC,OE,过点A作AF⊥CE于点F,可证得△ADC∽△ACB,△ACB∽△AFE,△ACF是等腰直角三角形,然后由相似三角形的对应边成比例以及勾股定理,即可求得答案.
解答 解:连接BC,OE,OC,过点A作AF⊥EC于点F,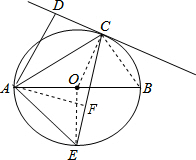 ∵直线CD与⊙O相切于点C,
∵直线CD与⊙O相切于点C,
∴OC⊥CD,
∵AD⊥CD,
∴OC∥AD,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠OAC=∠DAC,
即AC平分∠DAB;
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠ADC,
∵∠DAC=∠BAC,
∴△ADC∽△ACB,
∴$\frac{AD}{AC}=\frac{AC}{AB}$,
即$\frac{\frac{32}{5}}{8}=\frac{8}{AB}$,
解得:AB=10,
∴BC=$\sqrt{{AB}^{2}{-AC}^{2}}$=6,
∵点E为$\widehat{AB}$的中点,
∴∠AOE=90°,
∴OE=OA=$\frac{1}{2}$AB=5,
∴AE=$\sqrt{{OA}^{2}{+OE}^{2}}$=5$\sqrt{2}$,
∵∠AEF=∠B(同弧所对圆周角相等),∠AFE=∠ACB=90°,
∴△ACB∽△AFE,
∴$\frac{AB}{AE}=\frac{AC}{AF}$,
∴$\frac{10}{5\sqrt{2}}=\frac{8}{AF}$,
∴AF=4$\sqrt{2}$,EF=3$\sqrt{2}$,
∵∠ACF=$\frac{1}{2}$∠AOE=45°,
∴△ACF是等腰直角三角形,
∴CF=AF=4$\sqrt{2}$,
∴CE=CF+EF=7$\sqrt{2}$.
故选A.
点评 此题考查了切线的性质、相似三角形的判定与性质、勾股定理以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.


科目:初中数学 来源:2017届广东省南雄市九年级下学期模拟考试数学试卷(解析版) 题型:判断题
春季是流感的高发期,有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?如果按照这样的传染速度,三轮传染后有多少人患流感?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
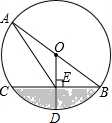 如图,已知AB是⊙O的直径,半径OD⊥BC于点E,连结AE,$\widehat{CD}$=60°.
如图,已知AB是⊙O的直径,半径OD⊥BC于点E,连结AE,$\widehat{CD}$=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com