练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．8袋花生，以每袋20千克为准，超过的千克数记作正数，不足的千克数记作负数，称重的记录如下：+0.3，+0.5，0，-0.4，-0.6，-0.3，+0.6，+0.7，8袋花生共超重或不是多少千克？总质量是多少千克？

    分析 “正”和“负”相对，超过的千克数记为正数，不足的千克数记为负数，把称重记录的数据相加，和为正说明超过了，和为负说明不足；求8袋花生的总重量，可以用8×20加上正负数的和即可．

    解答 解：（+0.5）+（+0.5）+0+（-0.4）+（-0.6）+（-0.3）+（+0.6）+（+0.7）=0.8（千克）．
    20×8+0.8=160.8（千克）．
    答：8袋花生共超重0.8千克，总重量是160.8千克．

    点评 本题考查了有理数的运算在实际中的应用．本题是把20千克看做基数，超过的记为正，不足的记为负，把正负数相加时，运用加法的运算律可简便运算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届广东省南雄市九年级下学期模拟考试数学试卷（解析版） 题型：单选题

    已知直线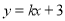经过点A（-1,2）且与X轴交于点B，点B的坐标是（ ）

    A. （-3,0） B. （0,3） C. （3,0） D. （0，-3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已如⊙O与⊙O′内切于A点，⊙O与⊙O′的半径分别为R和r（R＞r），P为⊙O上一点，PT切⊙O′于T点，连结AP交⊙O′于B点．求证：PA2：PT2=R：（R-r）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

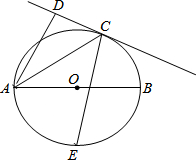    8．如图，AB是⊙O的直径，直线CD与⊙O相切于点C，AD⊥CD，垂足为D，E是弧AB的中点，若AD=$\frac{32}{5}$，AC=8，则CE的长为（　　）
    A．7$\sqrt{2}$B．7$\sqrt{3}$C．8$\sqrt{2}$D．3+4$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．一个等腰三角形的周长为15cm，一腰上的中线把周长分为两部分，这两部分的差为6cm，则腰长为（　　）
    A．$\frac{3}{2}$cmB．$\frac{3}{2}$cm或7cmC．7cmD．7cm或1cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

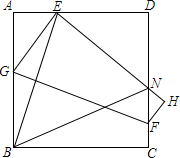    5．如图，四边形ABCD是正方形，E是AD边上一点，将正方形折叠，使点B与点E重合，FG是折痕，C点落在H上，EH与CD交于点N．求证：∠EBN=45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．在下列各图中都有AB∥CD，请你分别就下列图形，探究∠ABE、∠DCE、∠BEC之间的数量关系？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．阅读下列材料，然后回答问题．
    在进行二次根式的化简与运算时，我们有时会碰上如$\frac{2}{\sqrt{3}+1}$这样的式子，我们要用到分母有理化的方法将其化简：
    $\frac{2}{\sqrt{3}+1}$=$\frac{2×（\sqrt{3}-1）}{（\sqrt{3}+1）（\sqrt{3}-1）}$=$\frac{2（\sqrt{3}-1）}{{（\sqrt{3}）}^{2}-{1}^{2}}=\sqrt{3}-1$
    除了分母有理化，还可以用以下方法化简：
    $\frac{2}{\sqrt{3}+1}$=$\frac{3-1}{\sqrt{3}+1}=\frac{{（\sqrt{3}）}^{2}-{1}^{2}}{\sqrt{3}+1}=\frac{（\sqrt{3}+1）（\sqrt{3}-1）}{\sqrt{3}+1}=\sqrt{3}-1$
    （1）请用不同的方法化简$\frac{2}{\sqrt{5}+\sqrt{3}}$．
    （2）求$\frac{2}{\sqrt{3}+1}$+$\frac{2}{\sqrt{5}+\sqrt{3}}$+$\frac{2}{\sqrt{7}+\sqrt{5}}$+…+$\frac{2}{\sqrt{2n+1}+\sqrt{2n-1}}$的值（n为正整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．画出函数y1=2x-4与y2=-2x+8的图象，观察图象并回答问题：
    （1）x取何值时，2x-4＞0？
    （2）x取何值时，-2x+8＞0？
    （3）x取何值时，2x-4＞0与-2x+8＞0同时成立？
    （4）你能求出函数y1=2x-4与y2=-2x+8的图象与X轴所围成的三角形的面积吗？

    查看答案和解析>>

    同步练习册答案