
分析 (1)根据平方差公式,可得答案;
(2)根据平方差公式,可得答案.
解答 解:(1)$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\frac{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}{\sqrt{5}+\sqrt{3}}$=$\sqrt{5}$-$\sqrt{3}$;
$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}$=$\sqrt{5}$-$\sqrt{3}$;
(2)原式=$\sqrt{3}$-1+$\sqrt{5}$-$\sqrt{3}$+$\sqrt{7}$-$\sqrt{5}$+…+$\sqrt{2n+1}$-$\sqrt{2n-1}$
=$\sqrt{2n+1}$-1.
点评 本题考查了分母有理化,利用平方差公式是解题关键.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:解答题
如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
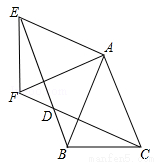
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
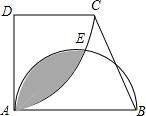 如图,∠D=∠DAB=90°,AD=CD=$\sqrt{3}$,AB=2,以D为圆心,AD为半径作扇形AEC,以AB为直径作半圆,则圆中阴影部分的面积为$\frac{5π}{6}-\sqrt{3}$.
如图,∠D=∠DAB=90°,AD=CD=$\sqrt{3}$,AB=2,以D为圆心,AD为半径作扇形AEC,以AB为直径作半圆,则圆中阴影部分的面积为$\frac{5π}{6}-\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com