Question

20．某工厂要加工一批密封罐，设计者给出了物体的如图所示的三视图，请你按照三视图确定制作每个密封罐所需钢板的面积（精确到1mm²）．

Answer 1

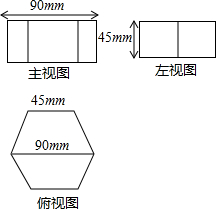
分析 根据三视图可以得出该几何体是正六棱柱，分别求出上下底的面积和侧面积，相加即可．

解答 解：易得组成六边形的六个正三角形的高为：$\frac{45\sqrt{3}}{2}$cm，
∴六边形的面积=6×$\frac{1}{2}$×45×$\frac{45\sqrt{3}}{2}$=$\frac{6075\sqrt{3}}{2}$cm²，
∴表面积=2×$\frac{6075\sqrt{3}}{2}$+6×45²≈22672（cm²），
答：制作每个密封罐所需钢板的面积约为22672cm²．

点评 本题考查了由三视图判断几何体的能力，由该三视图中的数确定正六棱柱的底面边长和高是解本题的关键，体现了数形结合的数学思想．