
分析 连接OA、0B,在OB上截取OM=AM,根据正多边形的性质、等腰三角形的性质和判定求出∠AOB=∠MAB,求出△OAB∽△ABM,得出关于a10的方程,求出方程的解即可.
解答 解:设AB是圆内接正十边形的一条边,则OA=OB=R,设AB=a10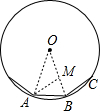 连接OA、0B,在OB上截取OM=AM,
连接OA、0B,在OB上截取OM=AM,
∵∠AOB=$\frac{360°}{10}$=36°,
∴∠OAM=∠AOB=36°,
∵OA=OB,
∴∠OAB=∠OBA=72°,
∴∠MAB=72°-36°=36°,
∴∠AMB=36°+36°=72°,
∴∠B=∠AMB,
∴AB=AM=OM=a10,
∵∠B=∠B,∠MAB=∠AOB,
∴△OAB∽△ABM,
∴$\frac{AB}{BM}$=$\frac{AO}{AM}$,
∴$\frac{{a}_{10}}{R-{a}_{10}}$=$\frac{R}{{a}_{10}}$,
∴a102+a10R-R2=0,
∴a10=$\frac{-1+\sqrt{5}}{2}$R(或$\frac{-1-\sqrt{5}}{2}$R不合题意舍弃).
∴a10=$\frac{1}{2}$($\sqrt{5}$-1)R.
点评 本题考查了正多边形和圆,相似三角形的性质和判定,正多边形的性质,等腰三角形的性质和判定的应用,解此题的关键是构造相似三角形,并进一步得出关于a10的方程,学会转化的思想,把问题掌握方程解决,难度适中.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:解答题
如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
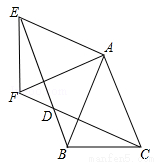
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com