练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，△ABC中，AB=AC=1，∠BAC=45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE、CF相交于点D．

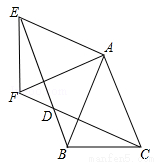
    （1）求证：BE=CF；

    （2）当四边形ACDE为菱形时，求BD的长．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

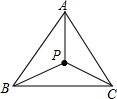    4．如图，点P是正△ABC内一点．
    （1）以点B为旋转中心，将△PBC逆时针旋转60°，试画出旋转后的图形；
    （2）若PB=3，PC=4，∠BPC=150°，请求出PA的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

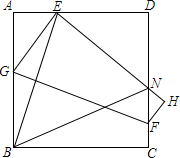    5．如图，四边形ABCD是正方形，E是AD边上一点，将正方形折叠，使点B与点E重合，FG是折痕，C点落在H上，EH与CD交于点N．求证：∠EBN=45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

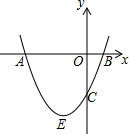    2．如图，抛物线y=x2+bx+c与y轴交于点C，与x轴交于点A，B，点A在点B的左侧，点A的坐标为A（-3，0），且AB=4．
    （1）求抛物线的解析式；
    （2）若过点C且与x轴平行的直线交抛物线于另一个点D，抛物线的顶点为点E，试判断△CDE的形状，并求其面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．阅读下列材料，然后回答问题．
    在进行二次根式的化简与运算时，我们有时会碰上如$\frac{2}{\sqrt{3}+1}$这样的式子，我们要用到分母有理化的方法将其化简：
    $\frac{2}{\sqrt{3}+1}$=$\frac{2×（\sqrt{3}-1）}{（\sqrt{3}+1）（\sqrt{3}-1）}$=$\frac{2（\sqrt{3}-1）}{{（\sqrt{3}）}^{2}-{1}^{2}}=\sqrt{3}-1$
    除了分母有理化，还可以用以下方法化简：
    $\frac{2}{\sqrt{3}+1}$=$\frac{3-1}{\sqrt{3}+1}=\frac{{（\sqrt{3}）}^{2}-{1}^{2}}{\sqrt{3}+1}=\frac{（\sqrt{3}+1）（\sqrt{3}-1）}{\sqrt{3}+1}=\sqrt{3}-1$
    （1）请用不同的方法化简$\frac{2}{\sqrt{5}+\sqrt{3}}$．
    （2）求$\frac{2}{\sqrt{3}+1}$+$\frac{2}{\sqrt{5}+\sqrt{3}}$+$\frac{2}{\sqrt{7}+\sqrt{5}}$+…+$\frac{2}{\sqrt{2n+1}+\sqrt{2n-1}}$的值（n为正整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．把下列二次根式化简最简二次根式：
    （1）$\sqrt{32}$；（2）$\sqrt{40}$；（3）$\sqrt{1.5}$；（4）$\sqrt{\frac{4}{3}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知：正十边形外接圆的半径为R．求证：正十边形的边长a10=$\frac{1}{2}$（$\sqrt{5}$-1）R．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

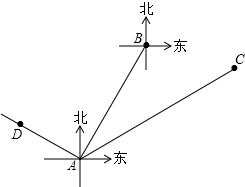    2．如图，在某海域内有A，C两个港口，港口C在港口A北偏东60°方向上，一艘船以每小时36海里的速度沿北偏东30°的方向驶离A港口，3小时后到达B点位置，在B处测得港口C在B处的南偏东75°方向上，求B处离港口C有多少海里．（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．计算：2-3=$\frac{1}{8}$，（-2）0=1，（$\frac{1}{2}$）-2=4．

    查看答案和解析>>

    同步练习册答案