
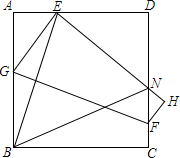
 如图,四边形ABCD是正方形,E是AD边上一点,将正方形折叠,使点B与点E重合,FG是折痕,C点落在H上,EH与CD交于点N.求证:∠EBN=45°.
如图,四边形ABCD是正方形,E是AD边上一点,将正方形折叠,使点B与点E重合,FG是折痕,C点落在H上,EH与CD交于点N.求证:∠EBN=45°. 分析 过B作BQ⊥EN,由△ABE≌△QBE,△BCN≌△BQN,从而可得到∠QBE=∠ABE,∠QBN=∠NBC,从而可知∠EBQ+∠QBN=$\frac{1}{2}$∠ABC=45°;
解答 证明:如图,过B作BQ⊥PH,垂足为Q.
∵GE=BG,
∴∠EBG=∠GEB.
又∵∠GEH=∠GBC=90°,
∴∠GEH-∠GEB=∠GBC-∠GBE.
即∠EBC=∠BEQ.
又∵AD∥BC,
∴∠AEB=∠EBC.
∴∠AEB=∠BEQ.
在△ABE和△QBE中,
$\left\{\begin{array}{l}{∠A=∠BQE}\\{∠AEB=∠BEQ}\\{BE=BE}\end{array}\right.$
∴△ABE≌△QBE(AAS).
∴∠ABE=∠QBE,AB=BQ,
又∵AB=BC,
∴BC=BQ.
又∵∠C=∠BQH=90°,BH=BH,
∴△BCH≌△BQH.
∴∠QBH=∠HBC,
∴∠EBN=∠EBQ+∠QBN=$\frac{1}{2}$∠ABC=45°.
点评 本题主要考查的是折叠的性质和全等三角形的性质和判定,证得两组三角形全等是解题的关键.


科目:初中数学 来源:2017届广东省南雄市九年级下学期模拟考试数学试卷(解析版) 题型:单选题
一个正多边形的内角是135°,这个多边形的边数是( )
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:解答题
如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
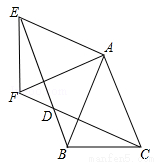
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com