
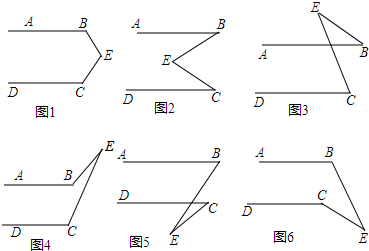
分析 分别过点E作EF∥AB,然后根据平行线的性质表示出∠BEF和∠DCE,再求解即可.
解答  解:过点E作EF∥AB,
解:过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
如图①,∠BEF=180°-∠B,∠CEF=180°-∠C,
∵∠BEF+∠CEF=180°-∠B+180°-∠C,
∴∠E=360°-∠B-∠C,
∴∠ABE+∠BEC+∠DCE=360°;
如图②,∠BEF=∠B,∠CEF=∠C,
∵∠E=∠BEF+∠CEF,
∴∠BEC=∠ABE+∠DCE;
如图③,∠CEF=180°-∠C,∠BEF=180°-∠B,
∵∠CEA=∠CEF-∠AEF,
∴∠CEA=(180°-∠DCE)-(180°-∠BAE)=∠BAE-∠DCE;
如图④,∠BEF=180°-∠ABE,∠CEF=180°-∠DCE,
∵∠BEC=∠BEF-∠CEF,
∴∠BEC=(180°-∠ABE)-(180°-∠DCE)=∠DCE-∠ABE;
如图⑤,∠BEF=180°-∠B,∠CEF=∠C,
∵∠CEF=∠BEF+∠CEB,
∴∠BEC=(180°-∠ABE)+∠C=180°-∠ABE+∠C,
∴∠ABE+∠BEC-∠C=180°;
如图6,∵∠BEF=180°-∠ABE,∠CEF=180°-∠C,
∴∠BEC=∠BEF-∠CEF=∠C-∠ABE.
点评 本题考查了平行线的性质,熟记性质是解题的关键,此类题目,难点在于过拐点E作平行线.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
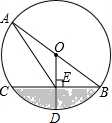 如图,已知AB是⊙O的直径,半径OD⊥BC于点E,连结AE,$\widehat{CD}$=60°.
如图,已知AB是⊙O的直径,半径OD⊥BC于点E,连结AE,$\widehat{CD}$=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
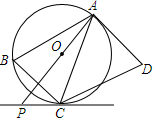 如图,四边形ABCD是平行四边形,⊙O是△ABC的外接圆,AD与⊙O相切于点A,AO的延长线与过点C的直线相交于点P,且∠PCB=∠ACD.
如图,四边形ABCD是平行四边形,⊙O是△ABC的外接圆,AD与⊙O相切于点A,AO的延长线与过点C的直线相交于点P,且∠PCB=∠ACD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com