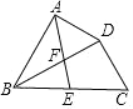
【题目】如图，在四边形ABCD中，BD平分∠ABC，∠BAD=∠BDC=90°，E为BC的中点，AE与BD相交于点F．若BC=4，∠CBD=30°，则DF的长为____
【答案】
【解析】
先在Rt△BDC中，利用锐角三角函数求出BD，再利用直角三角形的性质求出DE=BE=2，即：∠BDE=∠ABD，进而判断出DE∥AB，再求出AB=3，即可得出结论．
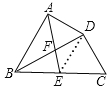
在Rt△BDC中，BC=4，∠DBC=30°，
∴cos∠DBC＝cos30°
∴BD=2
，
连接DE，
∵∠BDC=90°，点E是BC中点，
∴DE=BE=CE＝
BC=2，
∵∠DCB=30°，
∴∠BDE=∠DBC=30°，
∵BD平分∠ABC，
∴∠ABD=∠DBC，
∴∠ABD=∠BDE，
∴DE∥AB，
∴△DEF∽△BAF，
∴
，
在Rt△ABD中，∠ABD=30°，BD=2
∴AB=3，
∴
，
∴
，
∴DF=
，
故答案是：
科目：初中数学 来源： 题型：
【题目】问题：如图1，△ABC中，AB＝a，∠ACB＝α．如何用直尺和圆规作出点P，均使得∠APB＝
α？（不需解答）
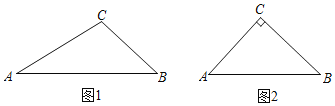
尝试：如图2，△ABC中，AC＝BC，∠ACB＝90°．
（1）请用直角三角尺（仅可画直角或直线）在图2中画出一个点P，使得∠APB＝45°
（2）如图3，若AC＝BC＝
，以点A为原点，直线AB为x轴，过点A垂直于AB的直线为y轴建立平面直角坐标系，直线y＝
（b≥0）交x轴于点M，交y轴与点N．
①当b＝7+
时，请仅用圆规在射线MN上作出点P，使得∠APB＝45°；
②请直接写出射线MN上使得∠APB＝45°或∠APB＝135°时点P的个数及相应的b的取值范围；
③应用：如图4，△ABC中，AB＝a，∠ACB＝α，请用直尺和圆规作出点P，使得∠APB＝α，且AP+BP最大，请简要说明理由．（不写作法，保留作图痕迹）
查看答案和解析>>
科目：初中数学 来源： 题型：
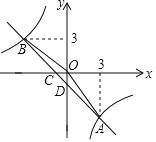
【题目】如图，一次函数y＝kx+b(k，b为常数，k≠0)的图象与反比例函数
的图象交于A、B两点，且与x轴交于点C，与y轴交于点D，A点的横坐标与B点的纵坐标都是3.
(1)求一次函数的表达式；
(2)求△AOB的面积；
(3)写出不等式kx+b＞﹣
的解集.
查看答案和解析>>
科目：初中数学 来源： 题型：
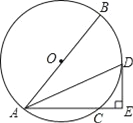
【题目】如图，已知⊙O的直径AB=10，弦AC=6，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC交AC的延长线于点E．
（1）求证：DE是⊙O的切线．
（2）求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
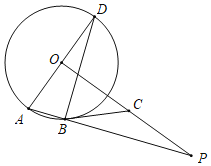
【题目】如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C．
（1）求证：∠CBP＝∠ADB；
（2）若OA＝4，AB＝2，求线段BP的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知抛物线y=x2+bx+c过A，B，C三点，点A的坐标是（3，0），点C的坐标是（0，-3），动点P在抛物线上．
（1）b =_________，c =_________，点B的坐标为_____________；（直接填写结果）
（2）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；
（3）过动点P作PE垂直y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，交BC于点D，过点E做直线l∥BC．
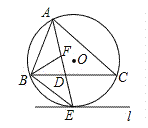
（1）判断直线l与⊙O的位置关系，并说明理由；
（2）若∠ABC的平分线BF交AD于点F，求证：BE=EF；
（3）在（2）的条件下，若DE=4，DF=3，求AF的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
