
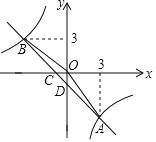
【题目】如图,一次函数y=kx+b(k,b为常数,k≠0)的图象与反比例函数![]() 的图象交于A、B两点,且与x轴交于点C,与y轴交于点D,A点的横坐标与B点的纵坐标都是3.
的图象交于A、B两点,且与x轴交于点C,与y轴交于点D,A点的横坐标与B点的纵坐标都是3.
(1)求一次函数的表达式;
(2)求△AOB的面积;
(3)写出不等式kx+b>﹣![]() 的解集.
的解集.
【答案】(1) y=﹣x﹣1;(2)△AOB的面积为![]() ;(3) x<﹣4或0<x<3.
;(3) x<﹣4或0<x<3.
【解析】
(1)先根据A点的横坐标与B点的纵坐标都是3,求出A,B,再把A,B的值代入解析式即可解答
(2)先求出C的坐标,利用三角形的面积公式即可解答
(3)一次函数大于反比例函数即一次函数的图象在反比例函数的图象的上边时,对应的x的取值范围;
(1)∵一次函数y=kx+b(k,b为常数,k≠0)的图象与反比例函数![]() 的图象交于A、B两点,
的图象交于A、B两点,
且与x轴交于点C,与y轴交于点D,A点的横坐标与B点的纵坐标都是3,
∴![]() ,
,
解得:x=﹣4,
y=﹣![]() =﹣4,
=﹣4,
故B(﹣4,3),A(3,﹣4),
把A,B点代入y=kx+b得:
![]() ,
,
解得:![]() ,
,
故直线解析式为:y=﹣x﹣1;
(2)y=﹣x﹣1,当y=0时,x=﹣1,
故C点坐标为:(﹣1,0),
则△AOB的面积为:![]() ×1×3+
×1×3+![]() ×1×4=
×1×4=![]() ;
;
(3)不等式kx+b>﹣![]() 的解集为:x<﹣4或0<x<3.
的解集为:x<﹣4或0<x<3.



科目:初中数学 来源: 题型:
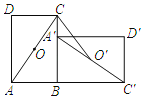
【题目】如图,在矩形ABCD中,O是对角线AC的中点.将ABCD绕点B顺时针旋转90°.旋转后的四边形为A'B′C′D',点A,C,D,O的对应点分别为A′,C',D',O’,若AB=8,BC=10,则线段CO’的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 过点(1,0)和点(0,-3),且顶点在第三象限,设m=a-b+c,则m的取值范围是( )
过点(1,0)和点(0,-3),且顶点在第三象限,设m=a-b+c,则m的取值范围是( )
A.-6<m<0B.-6<m<-3C.-3<m<0D.-3<m<-1
查看答案和解析>>
科目:初中数学 来源: 题型:
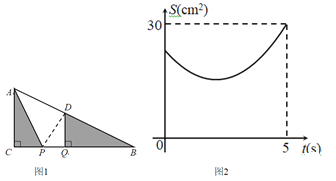
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6cm.点P、Q是BC边上两个动点(点Q在点P右边),PQ=2cm,点P从点C出发,沿CB向右运动,运动时间为t秒.5s后点Q到达点B,点P、Q停止运动,过点Q作QD⊥BC交AB于点D,连接AP,设△ACP与△BQD的面积和为S(cm),S与t的函数图像如图2所示.
(1)图1中BC= cm,点P运动的速度为 cm/s;
(2)t为何值时,面积和S最小,并求出最小值;
(3)连接PD,以点P为圆心线段PD的长为半径作⊙P,当⊙P与![]() 的边相切时,求t的值.
的边相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
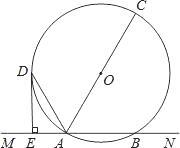
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
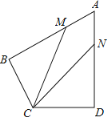
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2.则∠BCD= °,cos∠MCN= .
查看答案和解析>>
科目:初中数学 来源: 题型:
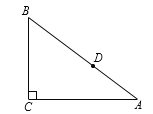
【题目】如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB边上一点(不与A、B重合),若过点D的直线截得的三角形与△ABC相似,并且平分△ABC的周长,则AD的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
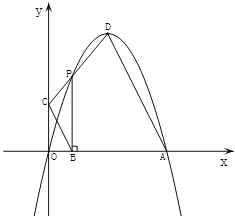
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,顶点
两点,顶点![]() 在第一象限,点
在第一象限,点![]() 在该抛物线上.
在该抛物线上.
(1)若点![]() 坐标为
坐标为![]() .
.
①求![]() 与
与![]() 的函数关系式;
的函数关系式;
②已知两点![]() ,
,![]() ,当抛物线
,当抛物线![]() 与线段
与线段![]() 没有交点时,求
没有交点时,求![]() 的取值范围;
的取值范围;
(2)若![]() 点在该抛物线的曲线段
点在该抛物线的曲线段![]() 上(不与点
上(不与点![]() ,
,![]() 重合),直线
重合),直线![]() 交
交![]() 轴于点
轴于点![]() ,过
,过![]() 点作
点作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
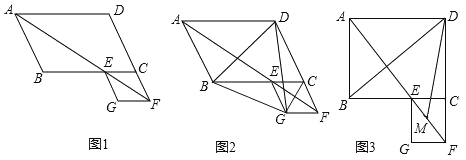
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作ECFG.
(1)如图1,证明ECFG为菱形;
(2)如图2,若∠ABC=120°,连接BG、CG,并求出∠BDG的度数:
(3)如图3,若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com