
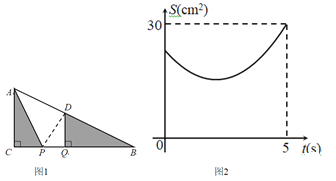
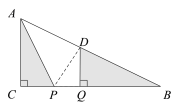
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6cm.点P、Q是BC边上两个动点(点Q在点P右边),PQ=2cm,点P从点C出发,沿CB向右运动,运动时间为t秒.5s后点Q到达点B,点P、Q停止运动,过点Q作QD⊥BC交AB于点D,连接AP,设△ACP与△BQD的面积和为S(cm),S与t的函数图像如图2所示.
(1)图1中BC= cm,点P运动的速度为 cm/s;
(2)t为何值时,面积和S最小,并求出最小值;
(3)连接PD,以点P为圆心线段PD的长为半径作⊙P,当⊙P与![]() 的边相切时,求t的值.
的边相切时,求t的值.
【答案】(1)12 , 2;(2)当t=2时,面积和S最小,最小为21cm2. (3)当t=1或![]() 时⊙P与△ABC的边相切
时⊙P与△ABC的边相切
【解析】
(1)根据题意知,点Q与点B重合时,△ACP的面积为30,依据三角形面积公式可得PC的长为10,由PQ=2得BC的长为12,根据“速度=路程÷时间”可求出点P的速度;
(2)分别求出PC=2t,BQ=10-2t,DQ=5-t,利用三角形面积公式得到二次函数关系式,进行配方即可求出最值;
(3)分⊙P与AB边和AC边相切两种情况进行分类讨论求解即可.
(1)当点Q与点B重合时,△ACP的面积=30,
∴![]()
∵AC=6cm,
∴PC=10cm,
∴BC=PC+PQ=10+2=12cm,
∴点P的速度为:10÷5=2(cm/s);
(2)由题可知PC=2t,BQ=12-2-2t=10-2t,
∵DQ⊥BC,AC⊥BC,
∴DQ∥AC,
∴△DQB∽△ACB,
∴![]() ,即
,即![]()
∴DQ=5-t
∴S=![]() =
=![]()
∴当t=2时,面积和S最小,最小为21cm2.
(3)⊙P与BC边不可能相切
i) ⊙P与AB边相切时△PQD∽△ACB,![]()
∴![]() ,
,
∴t=1
ii)⊙P与AC边相切时![]()
在Rt△PQD中,![]() ,
,
∴![]()
∴t=![]() 或t=
或t=![]() (舍去),
(舍去),
综上当t=1或![]() 时⊙P与△ABC的边相切.
时⊙P与△ABC的边相切.


科目:初中数学 来源: 题型:
【题目】随着城市化建设的发展,交通拥堵成为上班高峰时难以避免的现象.为了解龙泉驿某条道路交通拥堵情况,龙泉某中学同学经实地统计分析研究表明:当![]() 时,车流速度v(千米/小时)是车流密度x(辆/千米)的一次函数.当该道路的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为95辆/千米时,车流速度为50千米/小时.
时,车流速度v(千米/小时)是车流密度x(辆/千米)的一次函数.当该道路的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为95辆/千米时,车流速度为50千米/小时.
(1)当![]() 时,求车流速度v(千米/小时)与车流密度x(辆/千米)的函数关系式;
时,求车流速度v(千米/小时)与车流密度x(辆/千米)的函数关系式;
(2)为使该道路上车流速度大于40千米/小时且小于60千米/小时,应控制该道路上的车流密度在什么范围内?
(3)车流量(辆/小时)是单位时间内通过该道路上某观测点的车辆数,即:车流量=车流速度×车流密度.当![]() 时,求该道路上车流量y的最大值.此时车流速度为多少?
时,求该道路上车流量y的最大值.此时车流速度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=![]() x刻画.
x刻画.
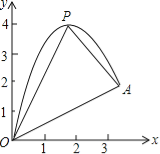
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果农在其承包的果园中种植了60棵桔子树,每棵桔子树的产量是100kg,果农想增加桔子树的棵数来增产,但增加果树会导致每棵树的光照减少,使得单棵果树产量减少,试验发现每增加1棵桔子树,单棵桔子树的产量减少0.5kg.
(1)在投入成本最低的情况下,增加多少棵桔子树时,可以使果园总产量达到6650kg?
(2)设增加x棵桔子树,考虑实际增加桔子树的情况,10≤x≤40,请你计算一下,果园总产量最多为多少kg,最少为多少kg?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校初三学生上周末使用手机的情况(选项:A.聊天;B.学习;C.购物;D.游戏;E.其他),随机抽查了该校初三若干名学生,对其上周末使用手机的情况进行统计(每个学生只选一个选项),绘制了统计表和条形统计图.
选项 | 人数 | 频率 |
A | 15 | 0.3 |
B | 10 | m |
C | 5 | 0.1 |
D | n | |
E | 5 | 0.1 |
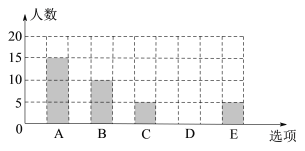
根据以上信息回答下列问题:
(1)这次调查的样本容量是 ;
(2)统计表中m= ,n= ,补全条形统计图;
(3)若该校初三有540名学生,请估计该校初三学生上周末利用手机学习的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1:y=2(x﹣3)2+1和抛物线y2:y=﹣2x2﹣8x﹣3,若无论k取何值,直线y=kx+km+n被两条抛物线所截的两条线段都保持相等,则m=_____,n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
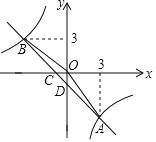
【题目】如图,一次函数y=kx+b(k,b为常数,k≠0)的图象与反比例函数![]() 的图象交于A、B两点,且与x轴交于点C,与y轴交于点D,A点的横坐标与B点的纵坐标都是3.
的图象交于A、B两点,且与x轴交于点C,与y轴交于点D,A点的横坐标与B点的纵坐标都是3.
(1)求一次函数的表达式;
(2)求△AOB的面积;
(3)写出不等式kx+b>﹣![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点H,点F是![]() 上一点,连接AF交CD的延长线于点E.
上一点,连接AF交CD的延长线于点E.
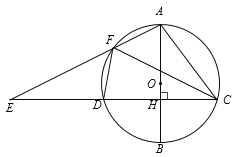
(1)求证:△AFC∽△ACE;
(2)若AC=5,DC=6,当点F为![]() 的中点时,求AF的值.
的中点时,求AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,点A(3,0),B(3,4).

(1)画出△AOB绕原点O逆时针旋转90°得到的△A'OB',并写出点A',B'的坐标;
(2)求线段AB在上述旋转过程中扫过的区域面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com