
【题目】某果农在其承包的果园中种植了60棵桔子树,每棵桔子树的产量是100kg,果农想增加桔子树的棵数来增产,但增加果树会导致每棵树的光照减少,使得单棵果树产量减少,试验发现每增加1棵桔子树,单棵桔子树的产量减少0.5kg.
(1)在投入成本最低的情况下,增加多少棵桔子树时,可以使果园总产量达到6650kg?
(2)设增加x棵桔子树,考虑实际增加桔子树的情况,10≤x≤40,请你计算一下,果园总产量最多为多少kg,最少为多少kg?
【答案】(1)增加10棵桔子树时收益可以达到6650kg.(2)果园最少产6650kg,最多产8000kg.
【解析】
(1)设增加x棵桔子树,根据“总产量=桔子树的平均产量×桔子树的棵” 列出方程解方程,再根据实际意义确定x的值;
(2)构建二次函数,利用二次函数性质解决问题.
(1)解:设增加x棵桔子树.
由题意得![]()
解之得x1=10,x2=130
∵成本最少,
∴x=10
答:增加10棵桔子树时收益可以达到6650kg.
(2)设总的收益为W
则W=![]() =
=![]() =
=![]()
∵10≤x≤40
∴当x=10时,Wmin=6650
当x=40时,Wmax=8000
答:果园最少产6650kg,最多产8000kg.


科目:初中数学 来源: 题型:
【题目】某服装店的员工与老板齐心协力,在2019年的经营中,每月的利润都在不断增加.该服装店的老板每季度都让员工总结经验与不足,下面是策划师与销售![]() 品牌服装的员工在第二季度总结的一部分.
品牌服装的员工在第二季度总结的一部分.
策划师的发言:第四月的利润为50万元,从第四月开始,第二季度的月增长率不变,第二季度的总利润为182万元.
销售![]() 品牌的员工发言:销售的
品牌的员工发言:销售的![]() 品牌服装在四月份中,进价为100元,售价为140元,每周销售60件,由于该服装进货量少,因此,采用涨价销售,每件涨1元时,平均每周少售2件,每周盈利2250元.
品牌服装在四月份中,进价为100元,售价为140元,每周销售60件,由于该服装进货量少,因此,采用涨价销售,每件涨1元时,平均每周少售2件,每周盈利2250元.

请根据总结解答相关的问题:
(1)求第二季度月增长率;
(2)![]() 品牌服装每周盈利2250元时,每件售价应该是多少元?
品牌服装每周盈利2250元时,每件售价应该是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(x0,m),Q(1,n)在二次函数y=(x+a)(x﹣a﹣1)(a≠0)的图象上,且m<n下列结论:①该二次函数与x轴交于点(﹣a,0)和(a+1,0);②该二次函数的对称轴是x=![]() ; ③该二次函数的最小值是(a+2)2; ④0<x0<1.其中正确的是_____.(填写序号)
; ③该二次函数的最小值是(a+2)2; ④0<x0<1.其中正确的是_____.(填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 过点(1,0)和点(0,-3),且顶点在第三象限,设m=a-b+c,则m的取值范围是( )
过点(1,0)和点(0,-3),且顶点在第三象限,设m=a-b+c,则m的取值范围是( )
A.-6<m<0B.-6<m<-3C.-3<m<0D.-3<m<-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的半圆O内有一条弦AC,点E是弦AC的中点,连接BE,并延长交半圆O于点D,若OB=2,OE=1,则∠CDE的度数是_______________.
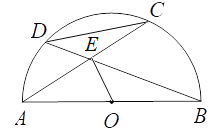
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6cm.点P、Q是BC边上两个动点(点Q在点P右边),PQ=2cm,点P从点C出发,沿CB向右运动,运动时间为t秒.5s后点Q到达点B,点P、Q停止运动,过点Q作QD⊥BC交AB于点D,连接AP,设△ACP与△BQD的面积和为S(cm),S与t的函数图像如图2所示.
(1)图1中BC= cm,点P运动的速度为 cm/s;
(2)t为何值时,面积和S最小,并求出最小值;
(3)连接PD,以点P为圆心线段PD的长为半径作⊙P,当⊙P与![]() 的边相切时,求t的值.
的边相切时,求t的值.
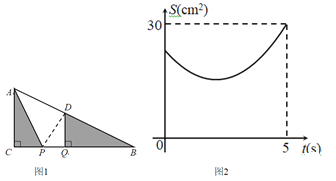
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2.则∠BCD= °,cos∠MCN= .
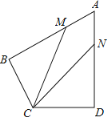
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在矩形ABCD中,AB=8,BC=x(0<x≤8),点E在边CD上,且CE=CB,以AE为对角线作正方形AGEF.设正方形AGEF的面积y.
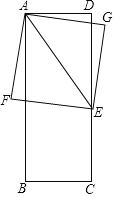
(1)当点F在矩形ABCD的边上时,x= .
(2)求y与x的函数关系式及y的取值范围.
(3)当矩形ABCD的一条边将正方形AGEF的面积分为1:3两部分时,直接写出x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com