
【题目】某服装店的员工与老板齐心协力,在2019年的经营中,每月的利润都在不断增加.该服装店的老板每季度都让员工总结经验与不足,下面是策划师与销售![]() 品牌服装的员工在第二季度总结的一部分.
品牌服装的员工在第二季度总结的一部分.
策划师的发言:第四月的利润为50万元,从第四月开始,第二季度的月增长率不变,第二季度的总利润为182万元.
销售![]() 品牌的员工发言:销售的
品牌的员工发言:销售的![]() 品牌服装在四月份中,进价为100元,售价为140元,每周销售60件,由于该服装进货量少,因此,采用涨价销售,每件涨1元时,平均每周少售2件,每周盈利2250元.
品牌服装在四月份中,进价为100元,售价为140元,每周销售60件,由于该服装进货量少,因此,采用涨价销售,每件涨1元时,平均每周少售2件,每周盈利2250元.

请根据总结解答相关的问题:
(1)求第二季度月增长率;
(2)![]() 品牌服装每周盈利2250元时,每件售价应该是多少元?
品牌服装每周盈利2250元时,每件售价应该是多少元?
科目:初中数学 来源: 题型:
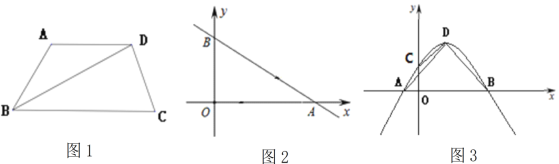
【题目】有一组邻边相等的凸四边形叫做“和睦四边形”,寓意是全世界和平共处,睦邻友好,共同发展.如菱形,正方形等都是“和睦四边形”.
(1)如图1,BD平分∠ABC,AD∥BC,求证:四边形ABCD为“和睦四边形”;
(2)如图2,直线![]() 与x轴、y轴分别交于A、B两点,点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发,设运动时间为t秒.当四边形BOPQ为“和睦四边形”时,求t的值;
与x轴、y轴分别交于A、B两点,点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发,设运动时间为t秒.当四边形BOPQ为“和睦四边形”时,求t的值;
(3)如图3,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B的左侧),与y轴交于点
轴交于A、B两点(点A在点B的左侧),与y轴交于点![]() ,抛物线的顶点为点D.当四边形COBD为“和睦四边形”,且CD=OC.抛物线还满足:①
,抛物线的顶点为点D.当四边形COBD为“和睦四边形”,且CD=OC.抛物线还满足:①![]() ;②顶点D在以AB为直径的圆上. 点
;②顶点D在以AB为直径的圆上. 点![]() 是抛物线
是抛物线![]() 上任意一点,且
上任意一点,且![]() .若
.若![]() 恒成立,求m的最小值.
恒成立,求m的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东55方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
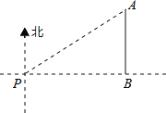
A.2cos55o海里B.![]() 海里C.2sin55海里D.
海里C.2sin55海里D.![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设D为锐角△ABC内一点,∠ADB=∠ACB+90°,过点B作BE⊥BD,BE=BD,连接EC.
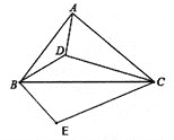
(1)求∠CAD+∠CBD的度数;
(2)若![]() ,
,
①求证:△ACD∽△BCE;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以AB为直径的圆交AC于点D,E是BC的中点,连接DE.
,以AB为直径的圆交AC于点D,E是BC的中点,连接DE.
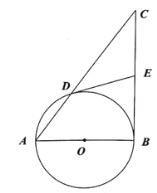
(1)求证:DE是![]() 的切线;
的切线;
(2)设![]() 的半径为r,证明
的半径为r,证明![]() ;
;
(3)若![]() ,求AD之长.
,求AD之长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着城市化建设的发展,交通拥堵成为上班高峰时难以避免的现象.为了解龙泉驿某条道路交通拥堵情况,龙泉某中学同学经实地统计分析研究表明:当![]() 时,车流速度v(千米/小时)是车流密度x(辆/千米)的一次函数.当该道路的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为95辆/千米时,车流速度为50千米/小时.
时,车流速度v(千米/小时)是车流密度x(辆/千米)的一次函数.当该道路的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为95辆/千米时,车流速度为50千米/小时.
(1)当![]() 时,求车流速度v(千米/小时)与车流密度x(辆/千米)的函数关系式;
时,求车流速度v(千米/小时)与车流密度x(辆/千米)的函数关系式;
(2)为使该道路上车流速度大于40千米/小时且小于60千米/小时,应控制该道路上的车流密度在什么范围内?
(3)车流量(辆/小时)是单位时间内通过该道路上某观测点的车辆数,即:车流量=车流速度×车流密度.当![]() 时,求该道路上车流量y的最大值.此时车流速度为多少?
时,求该道路上车流量y的最大值.此时车流速度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O交BC于点D,∠DAC=∠B.
(1)求证:CA是⊙O的切线.
(2)在AB上取一点E,若∠BCE=∠B,AB=2AC,求tan∠ACE的值.
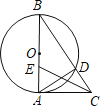
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果农在其承包的果园中种植了60棵桔子树,每棵桔子树的产量是100kg,果农想增加桔子树的棵数来增产,但增加果树会导致每棵树的光照减少,使得单棵果树产量减少,试验发现每增加1棵桔子树,单棵桔子树的产量减少0.5kg.
(1)在投入成本最低的情况下,增加多少棵桔子树时,可以使果园总产量达到6650kg?
(2)设增加x棵桔子树,考虑实际增加桔子树的情况,10≤x≤40,请你计算一下,果园总产量最多为多少kg,最少为多少kg?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com