
【题目】已知点P(x0,m),Q(1,n)在二次函数y=(x+a)(x﹣a﹣1)(a≠0)的图象上,且m<n下列结论:①该二次函数与x轴交于点(﹣a,0)和(a+1,0);②该二次函数的对称轴是x=![]() ; ③该二次函数的最小值是(a+2)2; ④0<x0<1.其中正确的是_____.(填写序号)
; ③该二次函数的最小值是(a+2)2; ④0<x0<1.其中正确的是_____.(填写序号)
【答案】①②④.
【解析】
(1)根据二次函数的解析式,求出与x轴的交点坐标,即可判断①;
(2)用与x轴交点的横坐标相加除以2,即可求证结论②;
(3)将二次函数交点式转化为顶点式,得到顶点坐标,即可求证③;
(4)讨论P点分别在对称轴的左侧和右侧两种情况,根据函数的增减性,计算x0的范围即可.
①∵二次函数y=(x+a)(x﹣a﹣1),
∴当y=0时,x1=﹣a,x2=a+1,即该二次函数与x轴交于点(﹣a,0)和(a+1,0).
故①结论正确;
②对称轴为:![]() .
.
故②结论正确;
③由y=(x+a)(x﹣a﹣1)得到:y=(x﹣![]() )2﹣(a+
)2﹣(a+![]() )2,则其最小值是﹣(a+
)2,则其最小值是﹣(a+![]() )2,
)2,
故③结论错误;
④当P在对称轴的左侧(含顶点)时,y随x的增大而减小,
由m<n,得0<x0≤![]() ;
;
当P在对称轴的右侧时,y随x的增大而增大,
由m<n,得![]() <x0<1,
<x0<1,
综上所述:m<n,所求x0的取值范围0<x0<1.
故④结论正确.
故答案是:①②④.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,设D为锐角△ABC内一点,∠ADB=∠ACB+90°,过点B作BE⊥BD,BE=BD,连接EC.
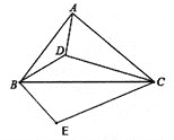
(1)求∠CAD+∠CBD的度数;
(2)若![]() ,
,
①求证:△ACD∽△BCE;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
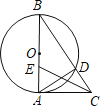
【题目】如图,在△ABC中,以AB为直径的⊙O交BC于点D,∠DAC=∠B.
(1)求证:CA是⊙O的切线.
(2)在AB上取一点E,若∠BCE=∠B,AB=2AC,求tan∠ACE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD,过点A作BC的垂线,垂足为点E,且满足AE=EC,过点C作AB的垂线,垂足为点F,交AE于点G,连接BG.

(1)如图1,若AC=![]() ,CD=4,求BC的长度;
,CD=4,求BC的长度;
(2)如图2取AC上一点Q,连接EQ,在△QEC内取一点,连接QH,EH,过点H作AC的垂线,垂足为点P,若QH=EH,∠QEH=45°.求证:AQ=2HP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=![]() x刻画.
x刻画.
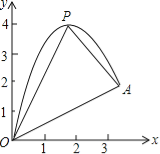
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标;
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2﹣4ax﹣5的开口向上.
(1)当a=1时,求抛物线与x轴的交点坐标;
(2)试说明抛物线C1一定经过两个定点,并求出这两个定点的坐标;
(3)将抛物线C1沿(2)所求的两个定点所在直线翻折,得到抛物线C2,
①写出抛物线C2的表达式;
②当抛物线C2的顶点到x轴的距离为2,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果农在其承包的果园中种植了60棵桔子树,每棵桔子树的产量是100kg,果农想增加桔子树的棵数来增产,但增加果树会导致每棵树的光照减少,使得单棵果树产量减少,试验发现每增加1棵桔子树,单棵桔子树的产量减少0.5kg.
(1)在投入成本最低的情况下,增加多少棵桔子树时,可以使果园总产量达到6650kg?
(2)设增加x棵桔子树,考虑实际增加桔子树的情况,10≤x≤40,请你计算一下,果园总产量最多为多少kg,最少为多少kg?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1:y=2(x﹣3)2+1和抛物线y2:y=﹣2x2﹣8x﹣3,若无论k取何值,直线y=kx+km+n被两条抛物线所截的两条线段都保持相等,则m=_____,n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
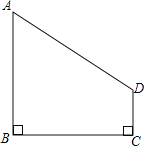
【题目】在四边形ABCD中,∠B=∠C=90°,若AB=4,BC=4,CD=1,问:在BC上是否存在点P,使得AP⊥PD?若存在,求出BP的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com