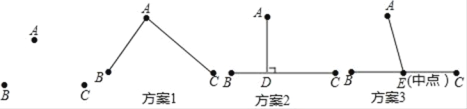
【题目】近年来，为减少空气污染，北京市一些农村地区实施了煤改气工程，某燃气公司要从燃气站点A向B，C两村铺设天然气管道，经测量得知燃气站点A到B村距离约3千米，到 C村距离约4千米，B，C两村间距离约5千米．下面是施工部门设计的三种铺设管道方案示意图．请你通过计算说明在不考虑其它因素的情况下，下面哪个方案所用管道最短．
科目：初中数学 来源： 题型：
【题目】问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°．求∠APC度数．
小明的解题思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠APC=50°+60°=110°．
问题迁移：
（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=∠α，∠BCP=∠β．试判断∠CPD、∠α、∠β之间有何数量关系？请说明理由；
（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我国有五座名山，但在洪雅人的心目中，我国有六座名山，这六座名山的海拔分别为：
山名 | 泰山 | 华山 | 黄山 | 庐山 | 峨嵋山 | 瓦屋山 |
海拔（米） | 1152 | 1997 | 1873 | 1500 | 1309 | 2830 |
（1）海拔最高的山是多少，最高的山与最低的山的海拔相差多少米；
（2）海拔不低于1500米的山的频数是多少；频率是多少；
（3）根据数据制作条形统计图．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现场学习：
在一次数学兴趣小组活动中，老师和几个同学一起探讨：在an=b中，a，b，n三者关系．
同学甲：已知a，n，可以求b，是我们学过的乘方运算，其中b叫做a的n次方．如：（﹣2）3=﹣8，其中﹣8是﹣2的3次方．
同学乙：已知b，n，可以求a，是我们学过的开方运算，其中a叫做b的n次方根．如：（±2）2=4，其中±2 是4的二次方根（或平方根）；（﹣3）3=﹣27，其中﹣3是﹣27的三次方根（或立方根）．
老师：两位同学说的很好，那么请大家计算：
（1）81的四次方根等于 ；﹣32的五次方根等于 ．
同学丙：老师，如果已知a和b，那么如何求n呢？又是一种什么运算呢？
老师：这个问题问的好，已知a，b，可以求n，它是一种新的运算，称为对数运算．
这种运算的定义是：若an=b（a＞0，a≠1），n叫做以a为底b的对数，记作：n=logab．例如：23=8，3叫做 以2为底8的对数，记作3=log28．根据题意，请大家计算：
（2）log327= ； （
）﹣2+
﹣log4
= ．
随后，老师和同学们又一起探究出对数运算的一条性质：如果a＞0，a≠1，M＞0，N＞0，那么logaMN=logaM+logaN．
（3）请你利用上述性质计算：log53+log5
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在数轴上，图中点A表示－36，点B表示44，动点P、Q分别从A、B两点同时出发，相向而行，动点P、Q的运动速度比之是3∶2（速度单位：1个单位长度/秒）．12秒后，动点P到达原点O，动点Q到达点C，设运动的时间为t（t＞0）秒．
（1）求OC的长；
（2）经过t秒钟，P、Q两点之间相距5个单位长度，求t的值；
（3）若动点P到达B点后，以原速度立即返回，当P点运动至原点时，动点Q是否到达A点，若到达，求提前到达了多少时间，若未能到达，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F，
， C△ABC=10cm且∠C=60°．求：
（1）⊙O的半径r；
（2）扇形OEF的面积（结果保留π）；
（3）扇形OEF的周长（结果保留π）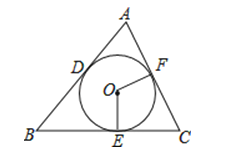
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了解学生对安全知识的掌握情况，学校随机抽取了20名学生进行安全知识测试，测试成绩(百分制)如下：
78、86、93、81、97、88、79、93、87、90、93、98、88、81、94、95、81、98、99、94
(1)根据上述数据，将下列表格补充完整（每组含最小值）：
成绩/分 | 70~80 | 80~90 | 90~100 |
人数 | 7 |
(2)若用(1)中数据制作扇形统计图，求出表示“70~80”扇形的圆心角度数；
(3)已知该校共有2000名学生，若规定成绩90分及以上为优秀，估计该校学生对安全知识掌握情况为优秀的有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，半径均为整数的同心圆组成的“圆环带”，若大圆的弦AB与小圆相切于点P，且弦AB的长度为定值
， 则满足条件的不全等的“圆环带”有（ ）
A.1个
B.2个
C.3个
D.无数个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
